 Links to the NRICH website Home page
Links to the NRICH website Home page

30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Cut it Out



- Problem
- Getting Started
- Student Solutions
- Teachers' Resources

The diagram shows an equilateral triangle dissected into 4 smaller equilateral triangles. Which numbers of smaller triangles are possible and which are not, and why? This remains a Tough Nut as nobody has yet explained why it is impossible to dissect an equilateral triangle into certain numbers of smaller equilateral triangles.
Robert and Andrew, St James Middle School, Bury St Edmund's sent this solution with six equilateral triangles. They say they think this is the only solution with 6 smaller triangles other than rotating the shape.
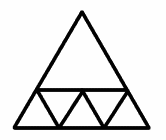
Talei and Stephanie of Poltair Community School and Sports College, St Austell, Cornwall said they think that dissection into 2 or 3 smaller triangles is impossible and that 4 is the smallest number of triangles possible. They gave this as an example of dissection into 15 smaller triangles.
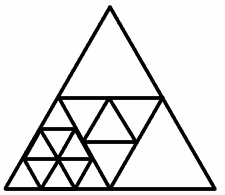
Talei's also had the idea of allowing overlapping triangles and realised that this would make it possible to have any number of smaller triangles, even infinitely many, but that would be a different question.
Lucas from St. Joseph's in Reading wrote in this wonderful explanation.
You may also like
Counting Counters
Take a counter and surround it by a ring of other counters that MUST touch two others. How many are needed?
Cuisenaire Squares
These squares have been made from Cuisenaire rods. Can you describe the pattern? What would the next square look like?
Consecutive Numbers
An investigation involving adding and subtracting sets of consecutive numbers. Lots to find out, lots to explore.