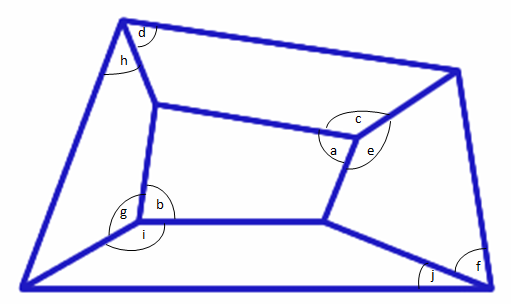
All five of the small quadrilaterals in the above shape are cyclic, and by using the fact that opposite angles in a cyclic quadrilateral add up to $180 ^{\circ}$ we can prove that the large quadrilateral made up of the five smaller ones is also cyclic.

Opposite angles in each cyclic quadrilateral add up to $180^{\circ}$, so we can write expressions for angles $a$, $c$, and $e$.

$$a = 180^{\circ}- b$$ $$c = 180^{\circ}- d$$ $$e = 180^{\circ}- f$$

Angles $a$, $c$, and $e$ are all round the same point therefore: $$360^{\circ} = a + c + e$$ Substituting in the expressions for angles c and e in we get: $$360^{\circ} = a + (180^{\circ} - d) + (180^{\circ} - f)$$

Simplifying this we get: $$360^{\circ} = a + 360^{\circ} - d - f$$ $$ a = d + f$$

Now we follow exactly the same working with the other side of the quadrilateral which gives us the equation $$b = h + j$$

We also know that $a + b = 180^{\circ}$ because they are opposite angles in a cyclic quadrilateral. Substituting in the expressions for $a$ and $b$ gives us $$d + f + h + j = 180^{\circ}$$

So $$(d + h) = 180^{\circ} - (f + j)$$

Looking back at the original diagram we can see that $(d + h)$ and $(f +j)$ are opposite angles in the quadrilateral and because $(d + h) = 180^{\circ} - (f + j)$ the quadrilateral must be cyclic.