Phase Space

 

In general, the gradient of a curve in phase space is $\frac{dv}{dx}$. 

For the first example, we have $$\frac{dv}{dx} \equiv 0 $$ As $v\equiv k >0$, this graph could represent the motion of a particle moving with constant velocity in the positive $x$-direction. Suppose the particle was at the origin at time $t=t_0$, then the motion would be given by $x = k(t-t_0)$. The particle would move from the left of the curve to the right.

 

In the second example, $x= x_0\sin(t)$, where $x_0$ is the maximum distance from the origin, would have the required phase space graph as $v = \frac{dx}{dt} =x_0\cos(t)$. The points $(x_0\sin(t), x_0\cos(t)$ form a circle as $t$ ranges from $0$ to $2\pi$. The particle would travel clockwise around the curve. 

 

The third example could represent a particle travelling with large velocity from the positive $x$-direction and being repelled by a particle of a charge with the same sign positioned at $x=-a, a>0$, a point more negative than any reached by the particle. The particle would travel along the bottom section of the graph from right to left and along the top section from left to right. 

 

The fourth example could be a particle starting with a positive velocity moving with constant deceleration from x=0 to x=k and then back to x=0. At this point, the sign of the acceleration suddenly changes, so it reaches x=-k with zero velocity and then accelerates to x=0 again. We can solve the equations to find the position in terms of time. 

Consider one of the four parts of the curve, suppose with $k>x,v>0$. The equation is $v= k-x$. We can write $v=\frac{dx}{dt}$ which implies $$\frac{dx}{dt} = k-x \Rightarrow t-t_0 = - \ln(k-x)$$ Inverting the formula gives $x = k - \exp(t_0 - t)$ and $v = exp(t_0 - t)$.

 

Consider the next section, with $x>0, v<0$. We have $v = x-k$, with $t_1- t = -\ln(k-x) \Rightarrow x = k - \exp(t-t_1)$.

 

The next section with $x<0, v<0$ we have $x+v = -k \Rightarrow \frac{dx}{dt} = -(k+x) \Rightarrow \ln(k+x) = t_2 - t \Rightarrow x = - k + \exp(t_0-t)$ and in the final section, $x = -k + \exp(t-t_3)$. $t_i$ are constants that give the correct boundary conditions. Can you draw a graph  showing the approximate behaviour? I think it would look something like this, where the red lines indicate where the sections start and end. It would repeat for ever as the path in the phase space is a closed loop!

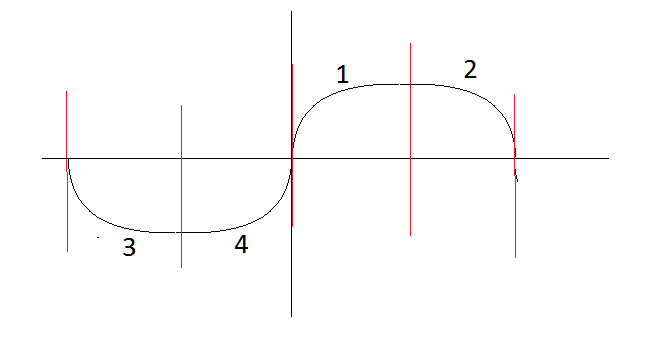
Graph E represents a particle moving from the negative-$x$ direction towards the origin with ever decreasing speed. It eventually reaches the origin, but takes a very long time.

 

Graph F shows a particle travelling from the origin with initially extremely high velocity, and the velocity decreases exponentially as it gets further from the origin.  

 

In general, all curves in the top half of the plane, with $v>0$, will travel from left to right, and all those in the bottom half of the plane, with $v<0$, will travel from right to left. A path which will take unit time for a particle to travel along will vary in length according to the values of $v$ along it. For small values of $v$, the path would be longer than it would be larger values of $v$. 

 

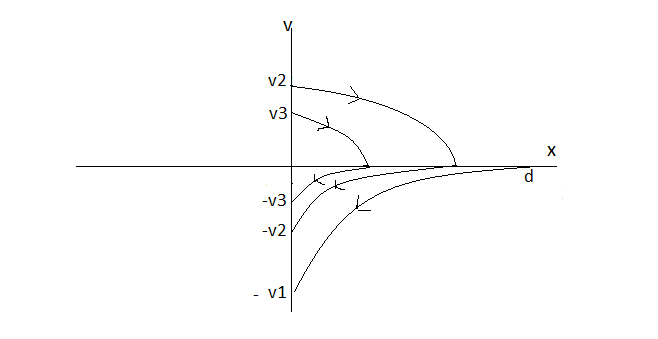
For the bouncy ball, the graph would look something like this, where the velocities $v_i$ are determined by the coefficient of restitution.