Forming an equation using the amounts added and subtracted

To shift the sequence along $D$ spaces,

from $(1111)+  (1112)+( 1113)+, \dots, (1111 + N-1)$
to $(1111+D)+(1112+D) + (1113+D) + \dots+(1111 + N -1+ D),$

you add $D$ to each term, so you add it $N$ times, since there are $N$ terms.
That is the same as adding a total of $N\times D$.

Then removing the first term, $1111+D$, takes the sum back to its original value.

So $N\times D$ must be equal to $1111+D$.
$$\begin{align}ND&=1111+D\\\Rightarrow ND-D&=1111\\\Rightarrow (N-1)D&=1111\end{align}$$
$N$ and $D$ are both integers, so $N-1$ and $D$ must be factors of $1111$.

$1111=11\times101$, which are both prime, so all of the possible values of $N$ and $D$ are shown below:

Product $(N-1)\times D =1111$	$N$ and $D$
$1111\times1$	$N=1112,D=1$
$1\times1111$	$N=2,D=1111$
$11\times101$	$N=12,D=101$
$101\times11$	$N=102,D=11$

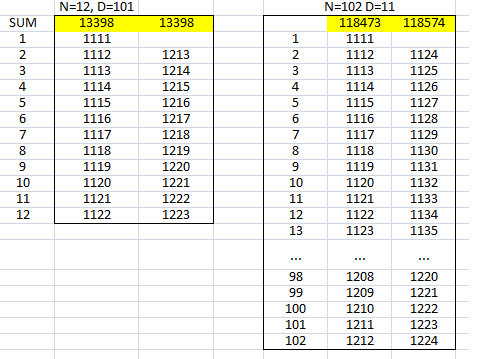
You can see some of these sums in action on the spreadsheet screenshot at the bottom of the page.


Using the formula for the sum of the first $n$ natural numbers

The sum of the first $n$ natural numbers is equal to $$
1+2+\dots + (n-1) + n =\frac{1}{2}n(n+1)
$$

Its easier in a problem like this to introduce some notation. Let's write $S(n)$ to mean the sum of the first $n$ natural numbers.
 
Since the two sums are equal we have
 
 
$$
S(1111+N-1)-S(1110) = S(1111+N -1 +D) - S(1111 + D)
$$
Let's put the formula into each of these and cancel each factor of a half.
$$
(1110+N)(1111+N)-(1110)(1111)=(1110+N+D)(1111+N+D)-(1111+D)(1112+D)
$$
Before leaping in we can see that many parts cancel, so we can put
$$
2221N + N^2 = 2221(N+D) + (N+D)^2 - 2223D - D^2- 2222 
$$
Collecting things together gives
$$
D(N-1) = 1111
$$
Now for a bit of number theory: $1111 = 11\times 101$, or $1\times1111$. Thus, for solutions we require:
$D = 11, N=102$ or $D=101, N=12$ or $D=1,N=1112$ or $D=1111,N=2$.
 
You can see some of these sums in action on this spreadsheet screenshot