Rocking chairs, railway games and rayboxes

 

When I got married, my mother gave me a case of woodworking tools. This was a bit of a surprise. No-one in the family did any woodworking and I'd done only a token amount at school. So the tools sat in the spare room gathering dust until after a year or two I felt sufficiently guilty to sign up for an evening class.

I turned up expecting to be told how to saw straight and perhaps make a few mortices and tenons. Instead the teacher gave me a cup of tea and sat me in an armchair. He gave me a pile of woodworking magazines and asked me what I wanted to make. By the end of the evening I was committed to making a rocking chair.

 

 

It took two years, but 45 years later the rocking chair still sits in our dining room (see left!) and every day reminds me to reflect upon his teaching. I'd expected laboriously to master a hundred different skills and finally be allowed to make something interesting. His approach was exactly the opposite: I'd start on something I wanted to make and whenever I needed a skill he'd teach me the technique.

What a wonderful learning experience that was. I saw myself as being the woodworking equivalent of innumerate; he believed everyone was capable of producing work fit to grace a living room. (And what a shame I never went to an evening class to learn the saxophone!)

It took me a shamefully long time to recognise the contrast between the way he taught woodwork and the way my colleagues and I taught mathematics. Rather than start from "What useful and interesting things can we do with mathematics?" we took the approach that only when children had adequately mastered a vast number of skills and routines might they at some ill-determined time in the future get around to doing something useful with their mathematics. Of course, the vast proportion of pupils leave school long before that point is reached, most of them never to touch the subject willingly again.

Someone once asked what the maths teachers' equivalent of my woodwork teacher's pile of magazines might be. The simple answer is that perhaps you're looking at it at this moment. Websites like NRICH offer more ideas than anyone can exploit in a whole career. Incidentally, I can flick through a book or magazine and get a good idea of what it has to offer in a couple of minutes, but it's by no means as easy on a screen. There's a book I've been wanting to read for nearly a year, but I've only got it as a series of Word chapters, and it looks as if it'll stay on the memory stick for a good while yet before I get around to it. And has anyone cracked the problem of just how you flick through a website? I've been doing some One-To-One tuition, and there are some Excel-based resources I know will be worth exploring, but there are - wait for it - one hundred of these. I'm lucky to have more time than most, but how does any ordinary mortal even flick through a hundred different programs?

For better or worse, websites weren't around in the first part of my teaching career, and by great good fortune I discovered a book that changed my life. (Actually it did so for a second time fifteen years later, but that's another story.) The book was Rex Walford's "Games In Geography" (ISBN: 0582320844 - as I write, there are copies available on Amazon for just 1p plus postage!). In the blink of an eye geography changed from being the most stultifyingly boring subject in the curriculum to the most exciting. Our school had a project week and I tried out one of the games. Over five afternoons a mixed-age, mixed-ability group was enthralled. Railroad Pioneers put children into situations where they had to discuss, reason, evaluate, make choices and decisions both tactically and strategically.

Much of the underlying structure of this and similar games was as much mathematical as geographical, and I eagerly devoured not only the games in this book but those of others working in the same field. Out of the blue I'd discovered activities in which decision-making, thinking ahead, discussion and real involvement were integral.

The games excited me for two reasons in particular. Firstly, because children were totally involved over extended periods, so involved they didn't even notice they were calling upon extensive amounts of mathematics. The high level of commitment meant that teachers needed to spend less time on managerial issues and could concentrate upon observing and helping children's learning, which was often at a considerably higher level than normal. I regularly saw children who I knew perfectly well were tackling a problem I knew they couldn't cope with. They failed to be intimidated or even recognise there were any difficulties and went on and solved the problem anyway.

Secondly, the maths had a purpose and a reality to the children. There's a story that's been told many times; it may not be true, but it certainly ought to be. A child goes home from school, to be asked "What did you do today?". "Well, in history we learnt about Christopher Columbus, in geography we did his journeys, in science we did an experiment to keep food fresh, in music we sang sea shanties, and in maths we did page 67, exercise 3!"

In other words, children don't have to be very old to have learned that mathematics isn't part of the real world; it's a collection of skills and routines that has no relevance at all to ordinary life and learning. I once spent a day in a school where I'd promised that no matter what each teacher was doing I'd develop some useful and interesting mathematics from it. All went pretty well, but with one class things were a bit stickier, and I was chatting to a group and racking my brains at the same time. We were talking about two things at once - about the ants in their formicarium, and how they used different dice in their Dungeons and Dragons games at home. Lightning struck, and ten minutes later we were using gridded paper and dice to simulate how ants searched for food. Another ten minutes and the whole class was involved, and so much came out of the topic that I had to contact the Natural History Museum for support. But what I remember above all else was the surprise of the children that they were able to use mathematics to do something meaningful - it really had never occurred to anyone that maths could contribute usefully to something interesting.

I once developed a month's maths around another railway building game, Railway Rivals (you can get full details from the inventor at davidgwynwatts@aol.com ). We built a map of the local area from hexagons, showing the major towns and geographical features like hills and rivers, and teams built railways which followed the actual historical routes with considerable accuracy. The map covered an entire wall and was very beautiful - visitors came from across the school to admire it - and one of my great regrets is that a teaching magazine lost the only photos. But a simulation doesn't have to demand lots of resources or visual materials. Rex Walford's Caribbean Fisherman is so simple and elegant that i's almost a work of art, and all you need is a single ordinary die. Yet I've used it with children at each of Key Stages 1, 2, and 3, and with 100+ teachers at a conference.

A remarkable feature of simulations is that you can add layer after layer of learning; they're a unique effective way of communicating ideas. In Caribbean Fisherman the fundamental idea is that a fisherman needs to decide whether the day is auspicious for taking his boat out for the day. And should I settle for the security of fishing close to shore, or should I go further out where the weather is more dangerous but the fish fetch higher prices? But before long questions will arise, and do so spontaneously. Surely if I've made a good catch on a day when others weren't prepared to go out then my fish should be worth more than on a day when plenty are landed? If I've already had two or three good days this week, do I need to go out on a day when the forecast is bad? And if you're out of action with damaged equipment you can't earn any money, so would co-operation between a group of us be a good idea? Or perhaps an insurance scheme might be sensible.

If the basic model is a good one, then a vast amount can be piled on top, and children assimilate far more than you could ask from any more conventional teaching programme. My Railway Rivals topic - done with the least-able group - began with hexagons and tessellations, took in costing the shortest and cheapest routes, diverted into probability and included a vast amount of arithmetic in developing the accounts needed. On top of that we learnt more about the local area than in a term of geography lessons - the towns and their different industries, and the reason why the main road, the bypass, the canal and the railway all run parallel and within a couple of hundred metres of each other.

Towards the end, the Divisional Education Officer looked in, and was a little sniffy. "Wouldn't it be better to look at what really happened rather than playing a simulation game?" she asked. The children were delighted to tell her just how closely their simulation had matched what had actually happened in the nineteenth century - the GWR route out to the west via Reading, the Great Northern out to Hitchin and Stevenage, and the Great Central out to Aylesbury. It's difficult to believe any conventional teaching programme could have matched the simulation for impact, enthusiasm, and quality of learning.

 

 

My degree subjects were chemistry and mathematics, so I was trained as a scientist. The scientist's job is find patterns in how things work, and to systematise and explain. Over the years I've used a number of very simple mathematical games to model processes of scientific exploration and discovery. You can get an idea of what I mean by trying See the Light. There's no simpler mathematical game than this. I've thought of a rule and you have to suggest numbers to try and gain insight into my rule. Try a few numbers and see how you get on- you can use any numbers you like (but you could try 5 and 10).

Well, clearly this is a mathematical game, but I'd suggest it tells you a lot about the processes of scientific exploration as well. I've put you in the position analogous to an experimenter attempting to unravel a scientific phenomenon. Perhaps you're trying various materials to discover what makes some magnetic and others not, or perhaps you're a researcher testing chemicals to see which make successful drugs. As the game goes on you're likely to experience a number of points with scientific relevance:

 

 

• Your early observations and theories are partial and incomplete, and your first enquiries may be based on little more than guesswork. Sooner or later you begin to get some idea of what may be going on, but you're still likely to have a very incomplete picture.
• It's very easy to get locked into an incorrect theory. For example you may keep thinking about multiples of five long after it's become clear this is in fact a red herring. (History is full of examples of scientists beguiled by attractive but totally wrong theories. Early chemists thought that when things burned, they gave out a substance called phlogiston into the air. Since we now know that burning uses oxygen from the atmosphere this theory couldn't be more wrong, but the phlogiston theory was still accepted a hundred years after there was ample evidence to disprove it. For that matter, there was a similar, and equally wrong, theory that when things get hot they do so because they have acquired a substance called caloric.)
• It's always possible to patch up an incorrect theory, however wrong. It's natural enough to assume the sun goes round the earth and does so in a circle, but as soon as detailed measurements were made the theory had to be amended to involve orbits with loops in. More accurate measurements required the loops themselves contained loops, but the theory still survived for hundreds of years before everyone accepted that in fact it's the earth which orbits the sun.
• Negative information - knowing that a particular number does not obey the rule - can be useful. And sometimes pure luck can help - there are many occasions when a chance observation led to important discoveries. Fleming's discovery of penicillin was built on capitalising upon a fortuitous speck of mould which redirected his researches into a whole new field. Becquerel discovered radioactivity when his photographic plates became mysteriously fogged. Similarly, Pasteur's work on immunology grew out of an experiment that went wrong because an assistant didn't perform his duties correctly.
• When you're trying to discover my rule your initial enquiries may be a bit hit-and-miss, but it becomes useful to work in an organised fashion - though you won't want to go as far as Mendel, whose laws of heredity were built on years of experiments which involved inspecting the characteristics of 300 000 peas. "Chance favours the prepared mind", said Pasteur.
• If we're modelling the scientific situation it's important I don't tell you what my rule is, because a scientist can never be sure s/he has achieved a perfect understanding; all you can ever say is that your idea fits with current evidence. There is always the possibility that someone will come along and produce an experiment or information which changes everything. Look at the history of the nature of the atom. For a long time atoms were envisaged as tiny solid spheres but a hundred years ago Rutherford performed an experiment in which tiny energetic particles almost invariably passed straight through a thin gold film - but about one in every 8000 didn't go though, and was bounced straight back. He compared the result to a piece of tissue paper bouncing an artillery shell backwards, and deduced that the atom was rather like a tiny solar system, with a central nucleus and orbiting electrons. Our picture of atomic structure has evolved considerably further since then, but there have been few better examples of how a single experiment changed our understanding overnight. (Our game may produce a similar change of perspective. When you've been thinking about my rule, you probably haven't discovered that $\pi$ obeys the rule, and this knowledge may require you to open up a whole new field of enquiry.)
• People often see science - and mathematics - as precise, cold, and logical, and this is the version that usually appears in the textbooks. What the textbooks miss out is all the human qualities - the confusion, the excitement, the wrong turnings and the red herrings. We forget that when Columbus journeyed to America he was trying to discover India and was so lost he was forced to keep a false log to convince his crew he knew what he was doing. James Watson's "The Double Helix" is a book I think everyone should read; it's the very personal account of how Watson and Crick unlocked the secret of DNA, and it communicates brilliantly that the scientists involved were not abstract superbeings but real people who made real mistakes.

 

 

 

The following problems on NRICH take the idea in See the Light a bit further: Light the Lights, Light the Lights Again, Charlie's Delightful Machine, Four Coloured Lights and A Little Light Thinking.

 

 

 

 

Individual atoms and molecules are so small that scientists cannot see them directly and have to explore them by indirect processes. Crick and Watson's discovery of the structure of DNA would have been made long before if it had been possible to look directly at the molecules. Instead they, and many other scientists, had to interpret photographs, not of the molecules themselves, but far larger aggregations.

One technique of exploring structure involves firing beams of sufficient energy to break the molecule into pieces. The makeup of the molecule is deduced by identifying the fragments and working out how they fit together. You can model this very simply with a game I call Fragments. The diagram shows a 16-section molecule - the sections are all connected horizontally or vertically.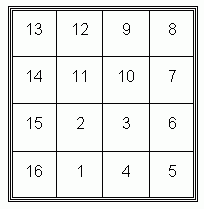

Image

You can use this game in a variety of versions, giving children a cut-up version of the diagram for them to reassemble it like a jigsaw. If just a small section of the molecule is broken off it's quite easy to reconstitute it, but if you break it into four 2x2 quarters (in this molecule the pieces will have cells numbered 11, 12, 13, 14; 7, 8, 9, 10; 1, 2, 15, 16; 3, 4, 5, 6), the reassembly is more difficult.

 

 

Can you reconstitute a similar, but differently arranged molecule, which breaks up into sections with numbers 1, 10, 15, 16; 2, 3, 4, 9; 5, 6, 7, 8; 11, 12, 13, 14?

And if you want a more intriguing puzzle still, I'll tell you that yet another similar, but differently arranged molecule, breaks up into four quarters - this time I won't tell you their component numbers, but that the products of the four numbers in each section are 24, 15288, 7920, 7200.

The game of White Box is based on using a less aggressive form of energy to acquire information. In this case the molecule is not broken up, but the positions of atoms within the crystal are deduced from observing which rays pass straight through, and which are deflected.

These games form part of a presentation linking maths and science which I've delivered many times in a variety of situations. They were designed to illuminate some of the processes in scientific discovery, but I want them also to offer something to mathematics teachers and pupils. I hope they carry the message that mathematics is a branch of knowledge which is not just a collection of techniques but which offers us the opportunity to pursue something we're positively interested in - just like woodwork, in fact.

 

Several of the games in this issue owe much to Richard Phillips, whose ideas I've tried to build upon over many years.