In mathematics it is often useful to have different ways of viewing concepts in order to help to build up intuition; however we need to know to what extent analogies are mathematically trust-worthy. Imagine the following proposals for analogies concerning calculus -- some might be good analogies, some might sometimes work and some might simply not work at all.

Consider and test these proposed analogies for understanding aspects of calculus carefully, applying them to several examples. Which analogies are largely sound, and which fail to work? Provide examples of functions to exemplify your points.


Analogy: A curve is a road on a map

Imagine an analogy where the curve of a function represents a road drawn on a map. Imagine driving along this road, starting from the left (west)



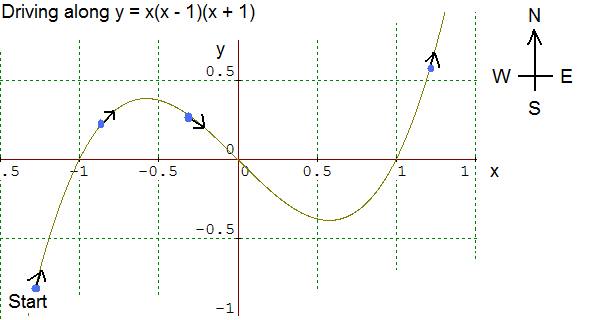
1. Sign of the derivative of a function at each point

The derivative of the function is positive when travelling towards the north, negative when travelling towards the south.


2. Sign of the second derivative of a function at each point

If your steering wheel is turned clockwise from the neutral position then the second derivative is negative. If it is turned anticlockwise from the neutral position then the second derivative at that point is positive.

3. Sign of the third derivative of a function at each point

If the steering wheel is in the process of turning in the anti clockwise direction then the third derivative is positive. If the steering wheel is in the process of turning in the clockwise direction then the third derivative is negative.

4. Differentiability condition at each point

The function is differentiable at points on the road when is it possible to drive along smoothly without having to suddenly turn the steering wheel.
 
5. Points of inflection
 
Points of inflection occur at the points, and only the points, where the steering wheel passes through the neutral position.

 
Note on terminology: The 'neutral position' is the position of the steering wheel in which the car travels forwards in a straight line. A clockwise turn from this position causes the car to turn right and an anticlockwise turn from this position causes the car to turn left.