You may also like

problem icon

Chocolate

There are three tables in a room with blocks of chocolate on each. Where would be the best place for each child in the class to sit if they came in one at a time?

problem icon

Plants

Three children are going to buy some plants for their birthdays. They will plant them within circular paths. How could they do this?

problem icon

Geometry and Gravity 1

This article (the first of two) contains ideas for investigations. Space-time, the curvature of space and topology are introduced with some fascinating problems to explore.

More Pebbles

Stage: 2 and 3 Challenge Level: Challenge Level:3 Challenge Level:3 Challenge Level:3

More Pebbles


This follows on from Pebbles. You may need to have a go at that problem first, it is intended for the most able pupils.

Now you are in a planet of no gravity. Pebbles placed in the air will stay there!
So, when we have eight pebbles we can form a cube in mid-air with a pebble at each vertex:


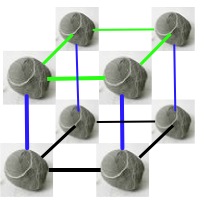
more pebs
(If you are struggling to see this, it might help to view the black lines as the bottom layer; blue lines as ascending edges; green lines as the top layer.)

We'll call this a cube of volume $1$.
Like the Pebbles activity, you have to add the smallest number of new pebbles to double the volume (rather than area) making cuboids (rather than rectangles) each time. Pebbles must be equidistant from the next ones in the same level. That is the pink, blue, green and black lines in the diagrams below need to be all the same length.

So, the next two could be as shown here.



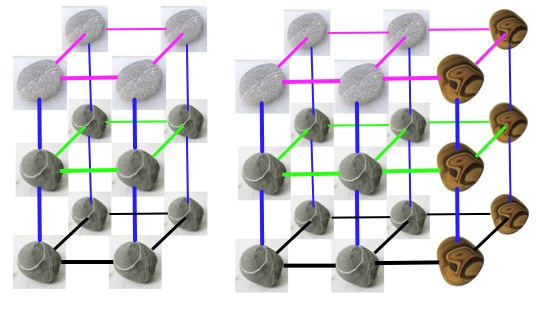
More more pebs
So remember:-
The rule is that you keep the pebbles that are there already (not moving them to any new positions) and add as FEW pebbles as necessary to DOUBLE the PREVIOUS volume. All have to be equidistant so the third one CANNOT be like this;

NOT


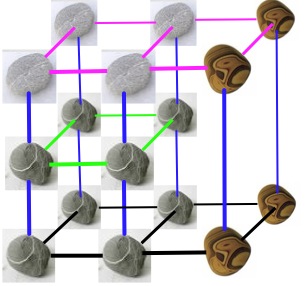
Well, now it's time for you to have a go.
 
"It's easy,'' I hear you say. Well, that's good.
But what questions can we ask about the arrangements that we are getting?
We could make a start by saying, "Stand back and look at the shapes you are getting. What do you see?''
I guess you may see quite a lot of different things. It would be good for you to do some more of this pattern. See how far you can go.

Well now, what about some questions to explore?
Here are some I've thought of that look interesting:
1. How many extra pebbles are added each time? This starts off $4, 6, 9,$ . . .
2. How many are there around the outside? This starts off $8, 12, 18,$ . . .
3. How many are there inside? This starts off $0, 0, 0,$ . . .
4. How big is the surface area? This starts off $6, 10, 16,$ . . .

Can you find a way of knowing how the numbers progress for these type of questions?

Try to answer these, and any other questions you come up with, and perhaps put them in a kind of table/graph/spreadsheet etc.
Do let me see what you get - I'll be most interested. Don't forget the all-important question you should ask - "I wonder what would happen if I ...?''

 

Why do this problem?

This activity is specially designed for the highest-attaining pupils that you ever come across. It acts as a further extension to Pebbles. It's an activity that is intended to give opportunities for those pupils to explore deeply using their intuition, flair and risk-taking skills.

Possible approach

It may be appropriate to make sure that the pupils have experienced Pebbles first and then, as this is designed for the highest attaining, it might be presented as on the website or in a one-to-one situation, encouraging discussion between adult and pupil. This discussion could determine what kind of start suits the learner, for example:
- maybe a model needs to be constructed,
- maybe a conversation about imagining it in the head,
- maybe a $2$D representation.
There are some kits with rods and balls that are magnets that could possibly be used to make the first models to help, as well as some construction materials that may usually be designed for the younger child.

Key questions

Tell me about this/your thinking.
How are you calculating/measuring the volume?


Possible extensions

These would have to come from the pupils' own suggestions and the directions that they find themselves in.
 


The NRICH Project aims to enrich the mathematical experiences of all learners. To support this aim, members of the NRICH team work in a wide range of capacities, including providing professional development for teachers wishing to embed rich mathematical tasks into everyday classroom practice. More information on many of our other activities can be found here.
Copyright © 1997 - 2012. University of Cambridge. All rights reserved.
NRICH is part of the family of activities in the Millennium Mathematics Project.