 Links to the NRICH website Home page
Links to the NRICH website Home page

30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Agile Algebra



- Problem
- Student Solutions
- Teachers' Resources
1. $(x + 3)^4 + (x + 5) ^4 = 34$
Nayanika from the Tiffin Girls' School in the UK solved this equation neatly, using a substitution. There is one small error which is corrected.
The solution is $x=-4\pm\sqrt2.$
2. $(x-1)(x-3)(x-5)(x-7)+15=0$
Nayanika used another substitution:
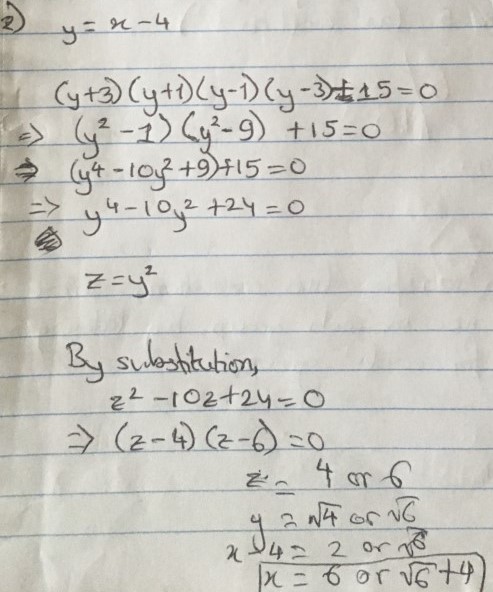
Remember that $y=-2,-\sqrt6$ are also solutions, which give $x=2, 4-\sqrt6$
3. $(x-4)(x-5)(x-6)(x-7)=1680$
Patrick from Woodbridge shool sent in this solution:
Let us rewrite the equation with $a = x-7$, then we have $(a+3)(a+2)(a+1)a = 1680.$
Note that $a(a+3) = a^2 + 3a$, and $(a+2)(a+1) = a^2 + 3a + 2$, so $(a+2)(a+1)(a+3)a = (a^2 + 3a)(a^2 + 3a + 2).$ Let us then take $y = a^2 + 3a$, then $y(y+2) = 1680$ and $y^2 + 2y - 1680 = 0.$
Factorising, we find $(y-40)(y+42) = 0$, so $y = -42$ or $+40$. Since $y = a^2 + 3a$, then we have either: $40 = a^2 + 3a$, so $(a+8)(a-5) = 0$ and $a = -8$ or $5$.
Alternatively $-42 = a^2 + 3a$, which has no real roots. Therefore, we have $a = -8$ or $5$. Then, since $a = x - 7$, $x = a + 7$, so $x = -1$ or $12$.
We will test this by substitution: $(-1-4)(-1-5)(-1-6)(-1-7)$, so for each bracket (-a-b) we can take out the negative to give -(a+b). There are four such brackets, so there are four -1 factors removed, which multiply to give 1. Therefore, $(1+4)(1+5)(1+6)(1+7) = 5\times 6\times 7\times 8 = 1680.$ Similarly, $x=12$ gives us $8\times 7\times 6\times 5 = 1680.$
Well done Patrick. An alternative substitution could be $t= x - 5\frac{1}{2}.$
Tom from The Skinners School used a substitution for the equation $x^4-8x^3 + 17x^2-8x+1=0,$ but it is not the one we suggested. Here is Tom's solution:
$f(x) = x^4 - 8x^3 + 17x^2 - 8x + 1 = 0$
use substitution $z = x^2 - 8x + 1$
so $f(x) = zx^2 + 15x^2 +z = 0$
use same substitution again for the $x^2$ term that is multiplied with $z$
$f(x) = z(z^2 + 8x - 1) + 15x^2 + z = 0$
$= z^2 + 8xz - z + 15x^2 + z$
$= z^2 + 8xz + 15x^2$
$= (z+3x)(z+5x)$
so $x^2 - 5x + 1 = 0$
and $x^2 - 3x +1 =0$
you can solve these quadratics using the quadratic equation and this gives you the four solutions to $f(x) = 0.$
Could the substitution we suggested, $z = x + \frac1x$ help with the next two equations?
4. $x^4-2x^3 -6x^2-2x+1=0$
5. $x^4-2x^3+2x^2-2x+1=0$
Tom also sent in a solution to the extension, $(8x+7)^2(4x+3)(x+1)=\frac{9}{2}$
let $y = x+1$
$(8y-1)^2(4y-1)(y) = \frac{9}{2}$
$(64y^2-16y+1)(4y^2-y) =\frac{9}{2}$
let $z = 4y^2 - y$
$(16z+1)(z) = \frac{9}{2}$
$16z^2 + z =\frac{9}{2}$
$32z^2 + 2z - 9 = 0$
$(2z-1)(16z+9) = 0$
Second bracket gives no real values of $y$ so for real solutions, $2z - 1 =0$
$z = \frac{1}{2}$
$4y^2 - y = \frac{1}{2}$
$8y^2 -2y -1=0$
$(4y+1)(2y-1)=0$
$y= -\frac{1}{4} \text{and} \frac{1}{2}$
$x = -\frac{5}{4} \text{and} -\frac{1}{2}$
You may also like
Cubic Spin
Prove that the graph of f(x) = x^3 - 6x^2 +9x +1 has rotational symmetry. Do graphs of all cubics have rotational symmetry?
Sine Problem
In this 'mesh' of sine graphs, one of the graphs is the graph of the sine function. Find the equations of the other graphs to reproduce the pattern.
Parabolic Patterns
The illustration shows the graphs of fifteen functions. Two of them have equations y=x^2 and y=-(x-4)^2. Find the equations of all the other graphs.