 Links to the NRICH website Home page
Links to the NRICH website Home page

30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
The Medieval Octagon



- Problem
- Student Solutions
Solution by: Andrew Ross from Dr. Challoner's Grammar School
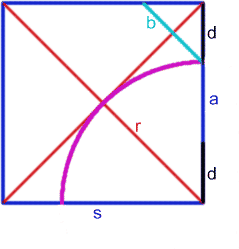
Call the side length of the square $s$. Use the diagram for other lengths.
The octagon has side lengths $a$ and $b$.
By Pythagoras' Theorem: $$r = {s\sqrt 2\over 2}$$ Because $s = r + d$ so $$d = s(1 - {\sqrt 2 \over 2}).$$ One side of the octagon is given by: $$a = s - 2d = s - 2s(1 - {\sqrt 2 \over 2}) = s(\sqrt 2 - 1).$$ By Pythagoras' Theorem $ b^2 = 2 d^2$ so $b = d \sqrt 2$. Hence $$b = s\sqrt 2 (1 - {\sqrt 2 \over 2}) = s(\sqrt 2 - 1) = a.$$ The octagon has rotational symmetry of order 4 as it was constructed from a square and all the sides are the same length, so it is a regular octagon.
You may also like
DOTS Division
Take any pair of two digit numbers x=ab and y=cd where, without loss of generality, ab > cd . Form two 4 digit numbers r=abcd and s=cdab and calculate: {r^2 - s^2} /{x^2 - y^2}.
Sixational
The nth term of a sequence is given by the formula n^3 + 11n. Find the first four terms of the sequence given by this formula and the first term of the sequence which is bigger than one million. Prove that all terms of the sequence are divisible by 6.