Links to the University of Cambridge website
 Links to the NRICH website Home page
Links to the NRICH website Home page

 Links to the NRICH website Home page
Links to the NRICH website Home page

Nurturing young mathematicians: teacher webinars
30 April (Primary), 1 May (Secondary)
30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
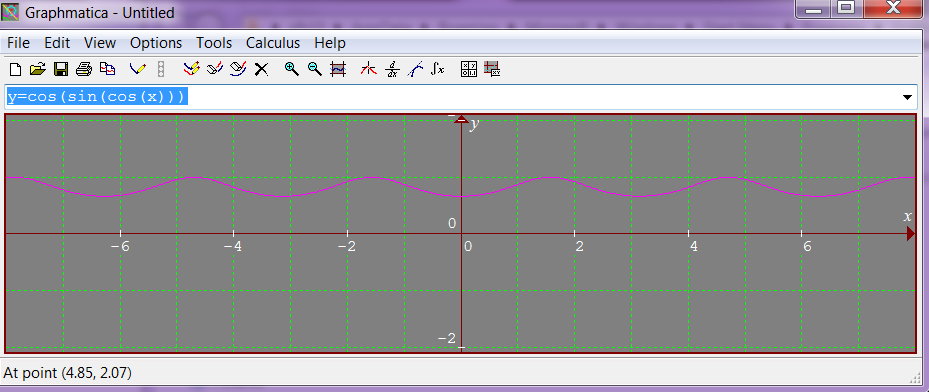
Trig Trig Trig
Age 16 to 18
ShortChallenge Level 





- Problem
- Solutions
Differentiating gives
$$f'(x) = \sin(\sin(\cos x)) \cdot \cos(\cos(x)) \cdot \sin(x)$$
This is zero if and only if
$$\sin(\sin(\cos x))=0 \mbox{ or } \cos(\cos(x)) = 0 \mbox{ or } \sin(x)=0$$
Consider the first of these three conditions:
$$\sin(\sin(\cos x))=0 \Rightarrow \sin(\cos x) = n\pi, n\in \mathbb{Z}$$
Since $|\sin(X)|\leq 1$ for any real $X$ and $\pi > 1$ we must choose $n=0$ in the previous equation.
Thus,
$$\sin(\sin(\cos x))=0 \Rightarrow \sin(\cos x) = 0 \Rightarrow \cos x = m\pi, m\in \mathbb{Z}$$
Similarly, we must choose $m=0$ in this expression. We can thus conclude that
$$\sin(\sin(\cos x))=0 \Leftrightarrow x = \left(r+\frac{1}{2}\right)\pi, r \in \mathbb{Z}$$
Consider the second of the three conditions:
$$\cos(\cos(x)) = 0 \Leftrightarrow \cos(x) = \left(r+\frac{1}{2}\right)\pi, r \in \mathbb{Z}$$
Since $\frac{1}{2}\pi> 1$ there are no real solutions to this condition.
Consider the third of the three conditions:
$$\sin(x) =0 \Leftrightarrow x = n\pi, n \in \mathbb{Z}$$
Combining all three conditions gives us the locations of the turning points:
$$
f'(x)=0 \Leftrightarrow x = \frac{N\pi}{2}, N\in \mathbb{Z}
$$
We now need to consider whether they are maxima, minima or something else. We could look at the second derivative, but this will be complicated and the boundedness of $\sin(x)$ and $\cos(x)$ allows us to make shortcuts as follows:
Notice that $f(x) = 1$ when $x = \pm \frac{\pi}{2}, \pm \frac{3\pi}{2}, \pm \frac{5\pi}{2}, \dots$. Since $f(x)$ is continuous and differentiable and $|f(x)|\leq 1$ these points must be maxima. The even multiples of $\frac{\pi}{2}$ must therefore be minima, at which the function takes the values $f(x) = \cos(\sin 1) \approx 0.666$.
A plot of the graph confirms this calculation: