Cube Bricks and Daisy Chains

'Cube Bricks and Daisy Chains' printed from https://nrich.maths.org/

Show menu

Cube Bricks and Daisy Chains

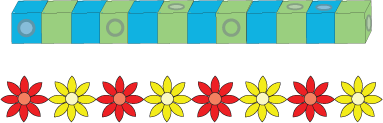
Daisy and Akram were making number patterns. Daisy was using beads that looked like flowers and Akram was using cube bricks. First they were counting in twos and their patterns looked like this:

Can you count along them in twos to see who made the longer one?

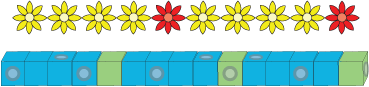
After this Daisy made another chain and Akram made another row of cubes.

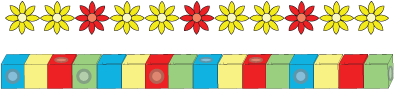
What were they counting in this time? After this they made more.

What was Daisy counting in this time? And what do you think Akram was doing with his cubes?

Can you make some chains and some rows of cubes counting in different numbers? You could use squared paper to help you draw the cubes.

Why do this problem?

This problem is designed for children early in their school lives. It gives a visual picture of counting in twos, fives etc. It is intended to be preceded by plenty of practical experience making patterns with beads, cubes etc.

Possible approach

You could introduce this activity by starting a string of beads or line of interlocking cubes making a pattern of twos. Ask the children what they notice and spend some time talking about the pattern, then invite individuals or pairs to continue it. You could ask the children how many cubes there are altogether and ask a few to count them. You could demonstrate counting in twos if the children themselves don't suggest it.

You could then move on to telling the group about Daisy and Akram. You could project the images on screen, print them from this sheet, or make them yourself.

When it comes to making their own 'chains', some children might like to use $2$ cm squared paper, or daisy chains can be coloured in on this sheet (which could be enlarged to A3 and cut into strips). Others will prefer to make chains from beads/cubes etc and you could take photographs of these as a record.

Encourage pupils to explain what they are doing, which number patterns they are making, and to count along the chains, rows etc that they have made. (It is interesting to note, that as children's understanding develops, their patterns can become 'simpler' and more easily described.)

At the end of the lesson the group should have an opportunity to share what they have been doing with each other, either using the actual materials or their recordings of them.

Key questions

What kind of pattern are you making? Tell me about it.

How could we count the number of cubes/flowers/beads ...?

Possible extension

Learners could be challenged to make much more complicated number patterns and write a few words to name each one.

Possible support

Some children will want to use cube bricks/beads etc and perhaps copy Daisy and Akram's patterns at first. Some may also prefer to keep their 'chains' rather than record them separately.