Copyright © University of Cambridge. All rights reserved.
'Torus Patterns' printed from https://nrich.maths.org/
Show menu
Why do this problem?
This problem gives a fascinating insight into topology and
various ideas from higher mathematics. It is ideal as a guided
class activity or a solitary workout for the more able maths
student. It will provide interesting insights to those interested
in pursuing mathematics beyond school.
The ideas raised in this problem would make for interesting
visual displays of mathematics.
Possible approach
The problem naturally splits into two parts. First it is
crucial that students will need to understand how the square
relates to the physical torus and then students can begin to
concentrate on the colouring aspect.
A good way to test understanding of the first part is to ask
students to give explanations of the setup to each other. Clear
explanations will give evidence of
understanding; students must realise that closed loops
drawn on the torus will yield lines which pass through opposite
points on the squares. You can draw some patterned squares which
don't give nice pictures on the torus to reinforce the point that
opposite sides on the squares are to be identified (some
suggestions are shown in the key questions).
The second part of the problem is best approached practically,
with students being encouraged to draw designs on squares and work
through the possible colourings. There are two levels of
sophistication that can be used. At one level students can draw
designs on the square and try to work out the minimal colouring.
(Note again that for a design to be valid, the lines must intersect
the opposite sides of the square at the correct corresponding
points.). At the highest level, students can try to
create patterns with the specific properties of needing 5, 6 and 7
colourings.
Although the thinking level in this problem is quite high, the
content level is relatively low; the problem could be attempted by
younger students, perhaps in a maths club context.
The design possibilities for this task are interesting, and
perhaps students could try to draw the designs from various squares
onto tori, or vice versa.
Key questions
Do you understand how the squares relate to tori? Can you see
why the images below don't give rise to closed loops on
tori?
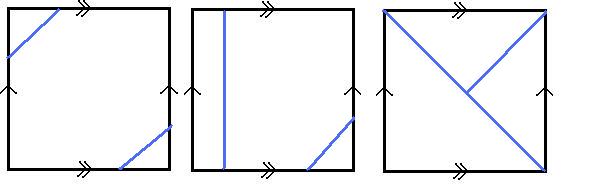
Possible extension
There are, in fact, no designs which need more than 7 colours
to fill. Although the proof will be beyond students, interested
students could research this idea on the internet. Alternatively,
students could try to find as many topologically different patterns
which require 7 colours to fill.
Possible support
You could first, or instead, try the problem Painting By
Numbers which raises many of the interesting colouring ideas of
this problem but without the problems raised by the topology of the
torus.