Copyright © University of Cambridge. All rights reserved.
'Torus Patterns' printed from https://nrich.maths.org/
Show menu
This problem naturally follows on
from Painting By Numbers, although it can be attempted
independently of this.
A torus may be represented by a square with the points on the two opposite sides identified.
In this problem we consider colouring in line drawings made on the surfaces of various tori.
They are to be coloured according to the two rules:
1) No two regions of the same colour can share a border
2) Two regions of the same colour are allowed to meet at a point.
Consider the following three patterns corresponding to three tori
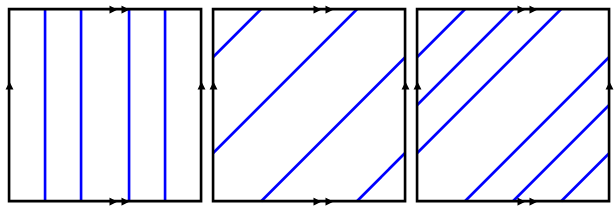
How many colours would be needed to colour the associated tori using the colouring rules above? You might wish to try to visualise the patterns on the tori, but this is not necessary.
Explore some other patterns on tori and how many colours would be needed to colour various patterns.
It is possible to create patterns which require 4, 5, 6 and 7 distinct colours to colour.
Can you create examples of such patterns?
Extension: Consider the question of painting by numbers on a Mobius strip
A torus may be represented by a square with the points on the two opposite sides identified.
In this problem we consider colouring in line drawings made on the surfaces of various tori.
They are to be coloured according to the two rules:
1) No two regions of the same colour can share a border
2) Two regions of the same colour are allowed to meet at a point.
Consider the following three patterns corresponding to three tori

How many colours would be needed to colour the associated tori using the colouring rules above? You might wish to try to visualise the patterns on the tori, but this is not necessary.
Explore some other patterns on tori and how many colours would be needed to colour various patterns.
It is possible to create patterns which require 4, 5, 6 and 7 distinct colours to colour.
Can you create examples of such patterns?
Extension: Consider the question of painting by numbers on a Mobius strip