Copyright © University of Cambridge. All rights reserved.
'L-triominoes' printed from https://nrich.maths.org/
Show menu
Why do this problem?
This problem begins with very simple ideas about tiling and enlargement but can lead learners to appreciate how proofs can be built up in stages, through breaking an idea down into special cases. It also introduces the intriguing mathematical notion of reptiles - shapes that can be tiled to make enlargements of themselves.Possible approach
Start by introducing the
smallest L-triomino and challenge learners to find a way to tile a
size 2, 3 and 4 L-triomino with it, on squared paper. They may work
in quite a haphazard way to start off with, and may not even find
ways of tiling them all. There is the opportunity to discuss the
number of tiles needed, and to make links with work on enlargements
and similar shapes.
Once everyone has had a
go at tiling the first few L-triominoes, and successful attempts
are collected on the board for all to see, follow up with: "I wonder whether all sizes of
L-triomino can be tiled"
Suggest the need for a
systematic approach, gradually building up knowledge of how
different sizes of L-triomino can be tiled.
Ask learners to start by
considering how the tiling of the size 2 L-triomino helps in tiling
the size 4 L-triomino. Can they develop their ideas further and
suggest how they would convince someone that all size $2^n$
L-triominoes can be tiled? Bring the class together to share their
insights.
Next, introduce the odd
numbered sizes of L-triominoes. Share these diagrams with the
class:
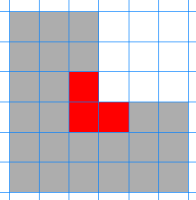
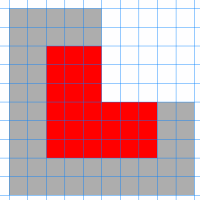
Challenge learners to
find simple ways of extending their tilings from one odd number to
the next, in a way that will lead to a convincing argument that all
odd sized L-triominoes can be tiled.
Finally, learners need to
consider how the two arguments can be combined to prove that all
L-triominoes can be tiled - this is a good opportunity to discuss
the formal steps in writing down a mathematical
argument.
Key questions
How can I use my
knowledge of tiling a size 2 L-triomino to tile a size 4?
How can I use my
knowledge of tiling a size 3 L-triomino to tile a size 5?
How can I use my
knowledge of tiling odd and $2^n$ sized L-triominoes to tile
ANY size L-triomino?
Possible extension
Investigate tilings with
these other reptiles:
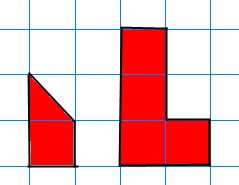
Come up with similar
proofs that all sizes can be tiled.