Floors and the ways that tiles are arranged have fascinated me for a long time. In different countries, cities and even small towns you find both walls and floors with interesting patterns.

I don't know about you but I find myself counting the tiles in particular ways. Maybe even your much younger brother or sister tends to count things that are around them. Keep your eyes open for patterns in tiles and you could discover a lot!

I was in an old church in Cambridge, where I live, and I looked at the floor.

This is what I saw:-

What a design!!

There were these things to count:-
. . . the tiles making up the three squares
. . . the dark green tiles that made a border for the squares
. . . the pale yellow tiles that filled in the gaps into the long rectangle.

When I got home I drew this design out (I had made some notes in the church, which is a good idea as it's sometimes hard to remember exactly how it was).

I then drew a 2 square version:-

and a 1 square!!

Well, it's really up to you to count and compare the numbers of particular tiles in one or all of these three designs.

See what number patterns you can come up with. I guess there are very many.

Now I wonder what would happen if we had four squares? I suppose we could put two lots of 2 together:-

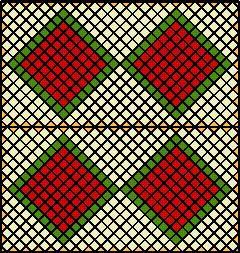
I was not altogether happy with this, but maybe you are, and that's O.K.

I decided to remove that centre line and come up with:-

Mind you, you could just continue with things in a straight line. What do you think?

Try this out for yourself and maybe extend the pattern for even greater numbers of squares.

Someone might be asking "What about smaller sized squares?" You then might have something like :-

You could try some more like these.
What rules do you decide on, so that the pattern works out in the same way?

Perhaps something rather different appears with different sized squares and you could follow that line!!

And for those who really are fed up with squares why not look at the same idea with triangles!!

Yes, here we are :-

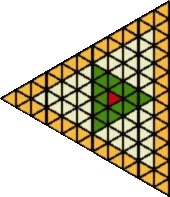
for the small one and my next size up is like this :-

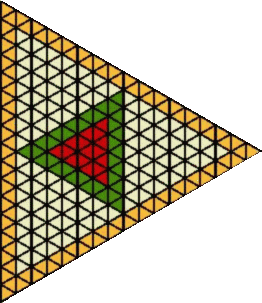
But what happens when we want more of the central triangles?

I wonder??