Links to the University of Cambridge website
 Links to the NRICH website Home page
Links to the NRICH website Home page

 Links to the NRICH website Home page
Links to the NRICH website Home page

Nurturing young mathematicians: teacher webinars
30 April (Primary), 1 May (Secondary)
30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Guessing the Graph
Age 14 to 16
Challenge Level 





- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
Preveina from Crest Girls' Academy sent us some thoughts:
I managed to fit a curve to the data. However when I tried generating new values it didn't fit within my curve so I had to draw another curve which fitted most of the points.
By using this graph you could answer scientific questions like:
Are there any anomalous results being produced?
What relationship can be described between the variables using the graph?
When does the graph reach its peak?
Herschel, from the European School of Varese sent us a well thought out solution:
When the complete set of data is plotted on a graph, it appears as three inverted parabolas, each in the general form $y = -ax^2+bx+c$. It suggests an object such as a bouncing ball, with the data showing its displacement or height.
The ball clearly bounces twice - once at about 0.65 seconds and again at around 1.25 seconds - and it loses height each time, due to the loss of kinetic energy at the point of impact. The drastic loss of energy with each successive bounce suggests that the surface is soft (such as carpet or grass) and that the ball is a (slightly deflated) football rather than a bouncy ball.
The ball or object starts from a height of 206 at the start, and it then reaches 47 after the first bounce and 15 after the third. If we assume these values to be in centimeters, we can work out the speed of impact on each of the third bounces with the formula $v=\sqrt{2gh}$, without accounting for air resistance. We see that the velocity upon the first impact is $6.35ms^-1$, $3.04ms^-1$ upon impact for the second time and $1.71ms^-1$ the third time - in other words, it loses half its speed each time it bounces.
We can also guess that it will reach a height of around 4cm after the 3rd bounce and around 1cm after the fourth, since the maximum height each time is approximately $\frac{1}{4}$ of the previous time - 75% of the ball's energy is lost in the form of sound and heat every time it bounces.
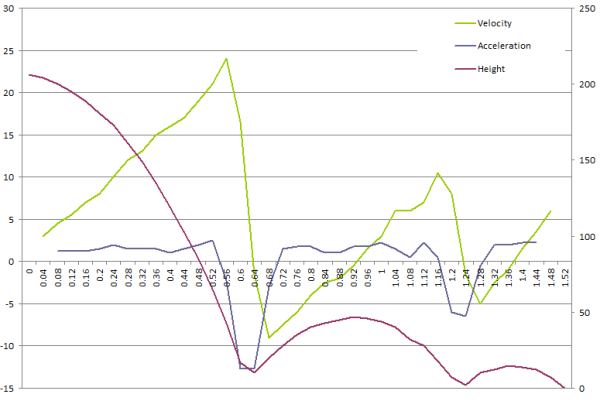
The graph plots height against time (i.e. the given data). There is also derived data, namely (downwards) velocity and acceleration. The original data (height) is on the right vertical axis while the derived data (velocity and acceleration) is on the left vertical axis, due to the difference in magnitudes of the values. Looking at the basic data, we see that the height curve is quite smooth, and the derived data shows that there is in fact a constant acceleration throughout the experiment, with the exception of the two points where the ball hits the ground and bounces. This is expected if it is a bouncing ball - it is under the constant force of gravity throughout the experiment.
A lovely analysis, Herschel - it was in fact a small plastic cube being dropped onto the carpet!