 Links to the NRICH website Home page
Links to the NRICH website Home page

30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Attractive Rotations



- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
Thank you to Sally and Emily from Parrs Wood for sending us pictures of their rotations. Here are their findings.
Sally noticed a pattern with the coordinates of our shape.
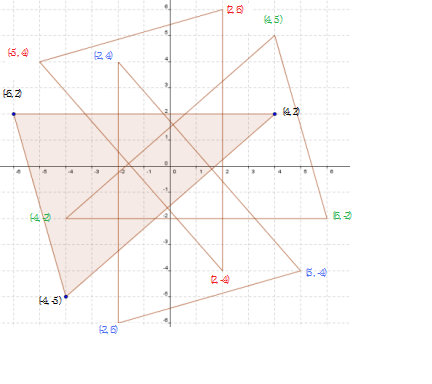
In the table below, the coordinates (x',y') describe where the points (x,y) end up after they have rotated by $90^\circ$ around (0,0):
| (x,y) | (x',y') |
| (-4,-5) | (-5,4) |
| (-6,2) | (2,6) |
| (4,2) | (2,-4) |
| (-5,4) | (4,5) |
| (2,6) | (6,-2) |
| (2,-4) | (-4,-2) |
| (4,5) | (5,-4) |
| (6,-2) | (-2,6) |
| (-4,-2) | (-2,4) |
| (5,-4) | (-4,5) |
| (-2,6) | (2,-6) |
| (-2,4) | (4,2) |
So the coordinates (x',y'), which are a rotation of (x,y) by $90^{\circ}$ around (0,0), are (y, -x).
$180^{\circ}$ rotation is just two $90^{\circ}$ rotations so
(x,y) $\longrightarrow$ (x',y') = (y,-x) $\longrightarrow$ (y',-x') = (-x, -y).
$90^{\circ}$ $90^{\circ}$

I predicted rotations of $30^{\circ}$ would have rotational symmetry of order 12 and $72^{\circ}$ would have rotational symmetry of order 5 because $360\div30 = 12$ and $360\div72 = 5$. These were true for the pictures I drew. I also knew I couldn't colour in my $72^{\circ}$ rotation shape because 5 is prime so its only factors are 5 and 1.
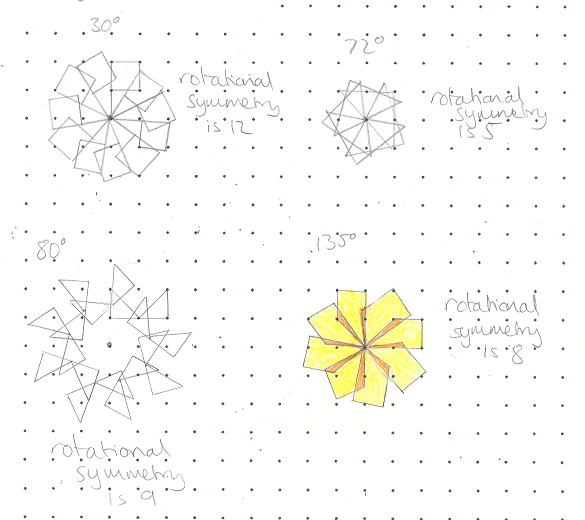
$360\div80 = 4.5$ and I had to go round twice to complete my shape. This then gave me rotational symmetry of order 9 because $360\times2=720$ and $720\div80 = 9$.
As $360\div135 = 2{2\over3}$, I worked out $360\times3=1080$ and $1080\div135 = 8$ so I knew I had to go round 3 times to get a shape with rotational symmetry.
Mr Bakker sent us a photo of the work some of his students did on this task:

Do continue sending us pictures of your rotation patterns along with any interesting mathematical discoveries you make.