You may also like

Illusion

A security camera, taking pictures each half a second, films a cyclist going by. In the film, the cyclist appears to go forward while the wheels appear to go backwards. Why?

Weighty Problem

The diagram shows a very heavy kitchen cabinet. It cannot be lifted but it can be pivoted around a corner. The task is to move it, without sliding, in a series of turns about the corners so that it is facing the other way round.

Rolling Triangle

The triangle ABC is equilateral. The arc AB has centre C, the arc BC has centre A and the arc CA has centre B. Explain how and why this shape can roll along between two parallel tracks.

Attractive Rotations

Age 11 to 14
Challenge Level

 

Why do this problem?

This problem provides a simple starting point creating attractive patterns using rotations, with the potential to go much further - exploring rotational symmetry, understanding the relationship between coordinates when rotating through multiples of $90^{\circ}$, and practising accurate construction with ruler, compasses and protractor are just a few ideas.

Work on this problem could provide an excellent opportunity for forging cross-curricular links with Art and Design departments.

 

Possible approach

These printable resources may be useful: Attractive Rotations,
                                                            Attractive Rotations Extension.

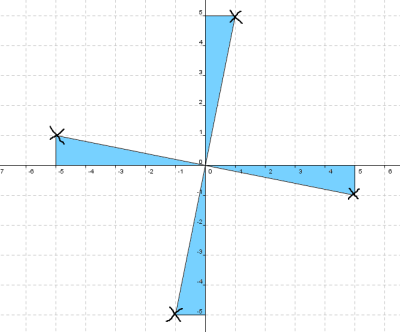
Begin by showing learners this image, and give them the chance to discuss in pairs anything they notice about it. Share ideas, and ask learners to suggest how they think the image might have been created.

 

Once they have had a chance to consider the symmetry of the image, show them the second image, which shows how the first image was made. Ask learners to create similar images of their own based on rotations through multiples of $90^{\circ}$ or through other angles using a protractor.

 

While they are constructing their own images, ask them to think of mathematical questions prompted by their images - these might include some of the lines of enquiry suggested below. Bring the class together during the lesson to share what they are choosing to work on, and at the end of the lesson to share their findings.

 

Key questions

How can you use a coordinate grid to help you to rotate each point through multiples of $90^{\circ}$ around $(0,0)$?

What is the relationship between the coordinates of the points as they rotate through multiples of $90^{\circ}$?

Can you use an isometric grid to rotate a shape through multiples of $60^{\circ}$?

What do you notice about the rotational symmetry of images based on rotations such as $30^{\circ}$ or $72^{\circ}$?

 

Possible support

Learners could begin by rotating single points through multiples of $90^{\circ}$ using the technique suggested below:
rotating a point through 90 degrees

 

Possible extension

What is the rotational symmetry of your final image if you rotate through multiples of $80^{\circ}$ or $135^{\circ}$?

Can you explain why?
Can you suggest other angles which would give similar effects?

 

 

 

 

 

 

The NRICH Project aims to enrich the mathematical experiences of all learners. To support this aim, members of the NRICH team work in a wide range of capacities, including providing professional development for teachers wishing to embed rich mathematical tasks into everyday classroom practice.
Copyright © 1997 - 2023. University of Cambridge. All rights reserved.
NRICH is part of the family of activities in the Millennium Mathematics Project.