Counting cogs
Which pairs of cogs let the coloured tooth touch every tooth on the other cog? Which pairs do not let this happen? Why?
Problem
This problem has been designed to be worked on in a group. For more details about how you might go about doing this, please read the Teachers' Notes.
Here are nine different cogs:
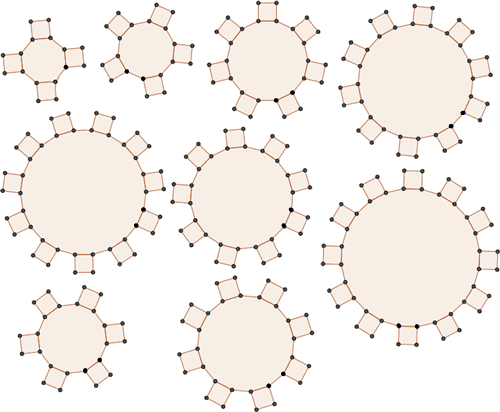
Take a pair of cogs. Mark a tooth on the first cog with a black dot. As the two cogs move around each other, note which gaps on second cog the marked tooth goes in to.
Here are some examples, where the first cog in the pair is one with six teeth.
When the second cog also has six teeth, the marked tooth only ever meets one of the six gaps on the second cog (the one also marked with a black dot):

When the second cog has seven teeth, the marked tooth meets each of the different coloured gaps on the second cog:
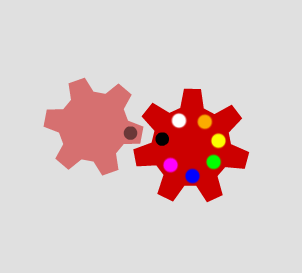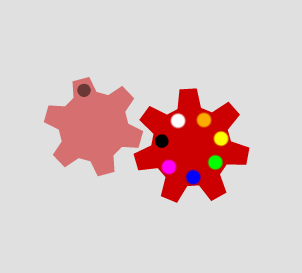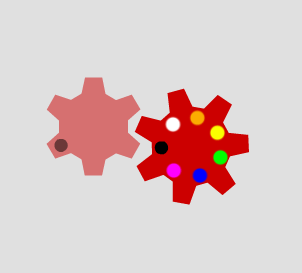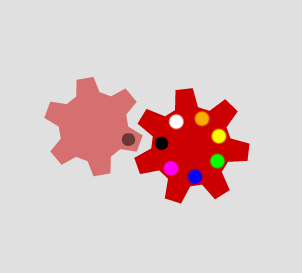
When the second cog has nine teeth, the marked tooth only goes in to the cogs marked with black or yellow dots:
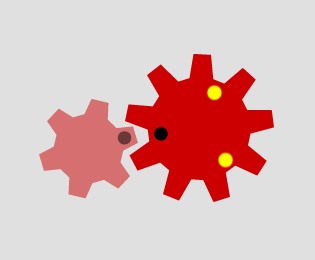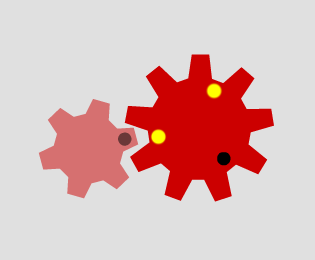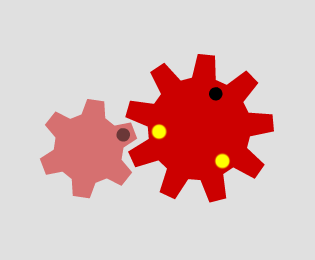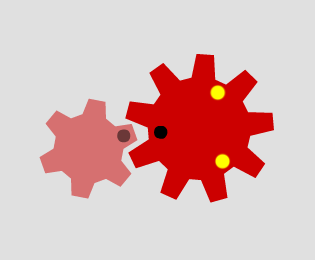
Which pairs of cogs let the coloured tooth go into every 'gap' on the other cog?
Which pairs do not let this happen? Why?
Can you explain how to determine which pairs will work, and why?
You could cut out the cogs from these sheets to try out your ideas.
Getting Started
Which pairs of cogs have you found that work?
Which pairs didn't work?
Do you get a sense of why?
What do you notice about the numbers of teeth in each case?
Student Solutions
Well done to everybody who had a go at this problem. We received an anonymous solution which said:
I notice that the space between the dots is the same number as the smaller cog. (For example, pairing the 12-cog with the 4-cog means that the marked tooth on the 4-cog goes into every fourth gap in the 12-cog.) So I have to find a number that the dots will be next to each other.
12 and 4 don't work but 5 and 6 work. I realised that 6-5=1, so the difference is one!
I start trying to prove this. 8-7=1 so I thought it would work. And I was right.
I decided to test some numbers that I predicted that won't work. 11-9=2. But it did!
This is very interesting. We received quite a few solutions from children who thought that two cogs with consecutive numbers would lead to the coloured tooth going into every 'gap', and those children often suggested that this wouldn't happen with two cogs with non-consecutive numbers. But as you've noticed, the 11-cog and the 9-cog do work! I wonder if there's something else going on with the numbers?
Dhruv from The Glasgow Academy in the UK looked at which cogs would let the the coloured tooth go into every gap when paired with the cog with six teeth. This picture can be clicked on to make it bigger:

Dhruv looked at the factors of the number of teeth of each cog, and noticed that the cogs that don't work when paired with the 6-cog share some factors (other than 1) with 6. This is an interesting observation - I wonder why this means that the coloured tooth won't go into every gap?
Shaunak from Ganit Manthan, Vicharvatika in India sent in this explanation and video:
Which pairs of cogs let the coloured tooth go into every 'gap' on the other cog?
If the numbers represent the number of teeth/gaps on each cog with the following notation, for example, the pairs in which the cogs let the coloured tooth of the first cog go into every gap on the other cog are:
(4, 5), (4, 7), (4, 9), (4, 11), (5, 6), (5, 7), (5, 8), (5, 9), (5, 11), (5, 12), (6, 7), (6, 11), (7, 8), (7, 9), (7, 10), (7, 11), (7, 12), (8, 9), (8, 11), (9, 10), (9, 11), (10, 11), (11, 12).
Which pairs do not let this happen? Why?
The pairs which will not work are:
(4, 4), (4, 6), (4, 8), (4, 10), (4, 12), (5, 10), (6, 6), (6, 8), (6, 9), (6, 10), (6, 12), (8, 8), (8, 10), (8, 12), (9, 9), (9, 12), (10, 10), (10, 12), (11, 11), (12, 12).
These pairs will not work because the tooth of the first cog touches only spots after a specific interval. This interval is the number of teeth on the first cog. If the HGF (highest common factor - the largest number that is a factor of both numbers) of the number of teeth on the first cog and the number of gaps on the second cog is x, then the coloured tooth will touch x gaps on the other cog.
If x = 1, then the coloured tooth will touch all gaps on the other cog.
This looks good, Shaunak - I think there is just one more pair that won't work, where both cogs have the same number of teeth.
Can you explain how to determine which pairs will work, and why?
The technique to figure out if a pair will work or not is as follows:
First, count the number of teeth on the first cog and the number of gaps on the second cog.
Next, find their HCF. If the HCF is 1, then the tooth will go on every other gap, else the pair will not work.
These are some good ideas, Shaunak! Thank you for sharing your method with us.
Thank you as well to Ahana, Sehar, Saanvi, Dhanvin, Aariz, Ananthjith, Vivaan, Sai, Pranathi, Paavani, Utkarsh and Dhruv from Ganit Kreeda, Vicharvatika in India, who all worked very hard on this problem. Take a look at Ganit Kreeda's full solution to see their ideas - they used the fact that the teeth on a cog go up to a certain number and then restart, like the numbers on a clock face do, to help them solve this problem.
Teachers' Resources
Why do this problem?
Many NRICH tasks have been designed with group work in mind. Here we have gathered together a collection of short articles that outline the merits of collaborative work, together with examples of teachers' classroom practice.
Possible approach
This is an ideal problem for learners to tackle in groups of four. Allocating these clear roles (Word, pdf) can help the group to work in a purposeful way - success on this task could be measured by how effectively members of the group work together as well as by the solutions they reach.
Introduce the four group roles to the class. It may be appropriate, if this is the first time the class has worked in this way, to allocate particular roles to particular children. If the class works in roles over a series of lessons, it is desirable to make sure everyone experiences each role over time.
For suggestions of team-building maths tasks for use with classes unfamiliar with group work, take a look at this article and the accompanying resources.
Give each group a copy of this sheet, which outlines the task. The idea is for them to read it together to find out what to do. Cut out a set of cogs for each group using this sheet and give them out so each person in a group has two or three cogs. Children should begin by working individually, investigating several pairs of cogs, then they will pool their findings as a group so that they have worked on all combinations of cogs.
Explain that each group will be expected to report back at the end of the session, showing the patterns they noticed, at least one conjecture they have and at least one question. Exploring the full potential of this task is likely to take more than one lesson, allowing time in each lesson for children to feed back ideas and share their thoughts and questions. Ask each group to record their reasoning, conjectures, explanations and any generalisations on a large sheet of paper (for example flipchart paper) in preparation for reporting back.
There are many ways that groups can report back. Here are just a few suggestions:
- Every group is given a couple of minutes to report back to the whole class. Learners can seek clarification and ask questions. After each presentation, children are invited to offer positive feedback. Finally, pupils can suggest how the group could have improved their work on the task.
- Everyone's posters are put on display at the front of the room, but only a couple of groups are selected to report back to the whole class. Feedback and suggestions can be given in the same way as above. Additionally, children from the groups which don't present can be invited to share at the end anything they did differently.
- Two children from each group move to join an adjacent group. The two "hosts" explain their findings to the two "visitors". The "visitors" act as critical friends, requiring clear mathematical explanations and justifications. The "visitors" then comment on anything they did differently in their own group.
Key questions
Which cogs have you found that work so far?
Which pairs didn't work? Can you explain why?
How could you predict whether a pair will work before you try them?
What questions would you like to ask?
Possible extension
Children could begin to work on a question that they have, or a question posed by another group.
Possible support
By working in groups with clearly assigned roles we are encouraging students to take responsibility for ensuring that everyone understands before the group moves on.
