Sorting the numbers
Complete these two jigsaws then put one on top of the other. What
happens when you add the 'touching' numbers? What happens when you
change the position of the jigsaws?
Age
5 to 11
Challenge level
Problem
Well how about doing a simple jigsaw ?
Image
This problem has been designed to be worked on in a group of about four. For more details about how you might go about doing this, please read the Teachers' Notes.
1. There are two jigsaw puzzles that your teacher can print out for you from here.pdf.
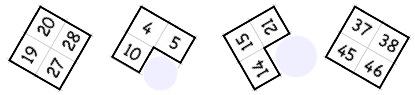
Complete each jigsaw and then put the pieces into the outline squares, which can be printed from here.pdf.
Image
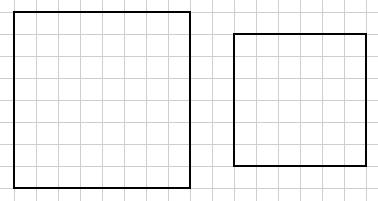
2. Place the smaller square of numbers on top of the other larger square in any way you like so that the small centimetre squares match up. (You may find it easier to copy the numbers on the smaller square onto a transparent sheet.)
3. Explore what happens when you add together the numbers that appear one on top of the other.
4. In your group, explore any other ideas that you come up with.
When you've looked at the thirty six combinations then you probably need to ask, "I wonder what would happen if we ...?". Change one small thing, explore that and then compare your two sets of results.
You might like to ask, "Why ...?".
Getting Started
What patterns or relationships have you come across?
Why are these relationships occurring?
What happens when you rotate the smaller/larger square?
What happens when you shift the smaller/larger square up or down?
Why are these relationships occurring?
What happens when you rotate the smaller/larger square?
What happens when you shift the smaller/larger square up or down?
Student Solutions
We had some interesting responses from St. James School in Southam. UK.
James, Mathieu, Morgan and Stephen wrote:
On the large square you add $8$ to each column and on the smaller square you add $6$ each time.
Alex, Isaac, Matty and Emil wrote:
$+8$ downwards, $+9$ diagonally right downwards, $+7$ diagonally left downwards
Lauren, Zoe, Jade and Katie:
The first box is equivalent to $22$, and then we discovered that if you plussed $8$, then that would be your next boxes answer! Following through right until the end of the larger square!
Finally from Leeds in the UK who sent in several neat thoughts, here's just one;
Image
Whilst this was all we had sent in it is probably the case that many of you did some interesting thinking about this but you felt that there was not anything that you could write into an email. Remember that whatever pieces of work come about from the starting point we are interested. LATE LATE NEWS:- Thank you Lady Elizabeth Hastings Primary School, Ledston for a truly wonderful response.
Teachers' Resources
Sorting the Numbers
Well how about doing a simple jigsaw ?
Image
This problem has been designed to be worked on in a group of about four. For more details about how you might go about doing this, please read the Teachers' Notes.
1. There are two jigsaw puzzles that your teacher can print out for you from here.
Complete each jigsaw and then put the pieces into the outline squares, which can be printed from here.
Image
2. Place the smaller square of numbers on top of the other larger square in any way you like so that the small centimetre squares match up. (You may find it easier to copy the numbers on the smaller square onto a transparent sheet.)
3. Explore what happens when you add together the numbers that appear one on top of the other.
4. In your group, explore any other ideas that you come up with.
When you've looked at the thirty six combinations then you probably need to ask, "I wonder what would happen if we ...?". Change one small thing, explore that and then compare your two sets of results.
You might like to ask, "Why ...?".
Why do this problem?
This problem offers learners the chance to explore their own questions, conjecture and possibly prove results. They will also be engaged in lots of calculating.
This activity lends itself to collaborative working, both for children who are inexperienced at working in a group and children who are used to working in this way. By working together on this problem, the task is shared and therefore becomes more manageable than if working alone.
Many NRICH tasks have been designed with group work in mind. Here we have gathered together a collection of short articles that outline the merits of collaborative work, together with examples of teachers' classroom practice.
Possible approach
This is an ideal problem for learners to tackle in groups of four. Allocating these clear roles (Word, pdf) can help the group to work in a purposeful way - success on
this task could be measured by how effectively members of the group work together as well as by their final solution. This version of the roles has been adapted for primary children.
Introduce the four group roles to the class. It may be appropriate, if this is the first time the class has worked in this way, to allocate particular roles to particular children. If the class works in roles over a series of lessons, it is desirable to make sure everyone experiences each role over time.
For suggestions of team-building maths tasks for use with classes unfamiliar with group work, take a look at this article and the accompanying resources.
You could give each group a copy of the two jigsaws and invite them to split into two pairs to start with, each pair working on one jigsaw. Once the jigsaws are complete, give out the blank grids and explain the rest of the task. It might be useful for each group to have a large sheet of paper on which they can record patterns and relationships they have noticed along with any explanations they have.
In the plenary, the whole class can share their findings so far. The discussion may reveal some patterns that can't be explained yet. If you post these up onto a wall in the classroom, then children can continue to work on the task during the coming week or even at home.
Key questions
If your focus is effective group work, this list of skills may be helpful (Word, pdf). Ask learners to identify which skills they demonstrated, and which
skills they need to develop further.
If your focus is mathematical, these prompts might be useful:
What ideas have you come up with and will you be able to share it with the whole class?
What patterns or relationships have you come across?
Why are these relationships occurring?
Possible extension
You can try a triangular arrangement so we might have a fifteen triangle placed on a thirty-six triangle:
Image
|
Image
|
You can print these triangles here.
Possible support
By working in groups with clearly assigned roles we are encouraging children to take responsibility for ensuring that everyone understands before the group moves on.