You may also like

problem icon

A Sameness Surely

Triangle ABC has a right angle at C. ACRS and CBPQ are squares. ST and PU are perpendicular to AB produced. Show that ST + PU = AB

problem icon

Three Balls

A circle has centre O and angle POR = angle QOR. Construct tangents at P and Q meeting at T. Draw a circle with diameter OT. Do P and Q lie inside, or on, or outside this circle?

problem icon

Angle Trisection

It is impossible to trisect an angle using only ruler and compasses but it can be done using a carpenter's square.

Encircling

Stage: 4 Challenge Level: Challenge Level:3 Challenge Level:3 Challenge Level:3

Congratulations James Page of Hethersett High School, Norwich on your solution to this question. Again there are many possible methods of showing that the radius of the circle is equal to the side of the square.



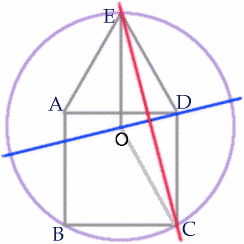
The blue line $OD$ is a diameter of the circle and a line of symmetry.

$\angle EDC = 150^{\circ}$ and $\triangle ECD$ isosceles so $\angle CED = \angle CDE =15^{\circ}$.

Now $\angle OED = 30^{\circ}$ so $\angle OEC = \angle OED - \angle CED = 15^{\circ}$ and hence the red line $EC$ is a line of symmetry for the quadrilateral $OEDC$ proving that the radius of the circle, $OC$ is equal in length to the side of the square.
The NRICH Project aims to enrich the mathematical experiences of all learners. To support this aim, members of the NRICH team work in a wide range of capacities, including providing professional development for teachers wishing to embed rich mathematical tasks into everyday classroom practice. More information on many of our other activities can be found here.
Copyright © 1997 - 2012. University of Cambridge. All rights reserved.
NRICH is part of the family of activities in the Millennium Mathematics Project.