Links to the University of Cambridge website
 Links to the NRICH website Home page
Links to the NRICH website Home page

 Links to the NRICH website Home page
Links to the NRICH website Home page

Nurturing young mathematicians: teacher webinars
30 April (Primary), 1 May (Secondary)
30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Table Patterns Go Wild!
Age 7 to 11
Challenge Level 





- Problem
- Getting Started
- Submit a Solution
- Teachers' Resources
Table Patterns Go Wild!
Nearly all of us have made table patterns on hundred squares, that is $10$ by $10$ grids. Some tables made vertical lines, some made diagonal lines and some patterns ranging across the whole space. Hundred squares are $10$ by $10$ grids. In this problem we will call these "$10$ grids".

What numbers made which sort of patterns and why?
This problem looks at the patterns on differently sized square grids. These are from $4$ grids (that is a $4$ by $4$ grid) to $9$ grids.
These are patterns on a $7$, a $5$, an $8$ and on a $6$ grid:
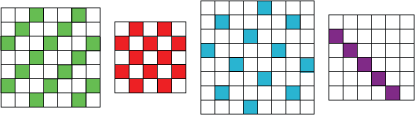
What tables made these patterns? Can you think why they made them like that?
Perhaps this is the time to experiment for yourself. You can use grids drawn on squared paper or use this sheet.
Can you discover what makes vertical and diagonal lines on the different grids and what makes the various patterns. Can you make the checked pattern? What table do you need to use on what kind of grid?
Here are the top parts of some grids.
Can you identify what table on what grid have been used to make them?

Here are some parts of various grids. This time we have not shown the edges of the grids. Can you identify what tables on what grids could have been used to make these patterns?

There may be more than one answer.
Why do this problem?
This problem helps to extend learners' familiarity with factors as well as providing interesting work on multiplication tables. They can make hypotheses, and test them in a simple and easily understood environment. It provides an opportunity to introduce the idea of a letter standing for "any number".
It can also add to their ideas of pattern and design.
Possible approach
If learners have not done many table patterns on hundred squares you could start by doing some of these. It is important that they do not see these as a series of straight lines, so it is advisable to get them to do the three times and four times tables before they embark on the two and five times. They should be asked why the tables of twos and fives make straight lines. Of course the word
"factor" might pop up here and there.
If plenty of work has already been done on in this area ask what makes straight vertical lines and why. Next give out unnumbered $10$ grids (on this sheet or on squared paper) and get different learners to do
different numbers so all are done, asking them to predict what sort of pattern they think they will get. It is advisable to suggest putting crosses on the appropriate squares as colouring them in can take a long time!
After this introduce the different grids. They can be found on this sheet. Learners could work in pairs to share each other's findings and also discuss their ideas with a partner.
There are two photocopiable "problem sheets" for learners to identify the tables and grids. These have more on them than the ones given in the problem. This sheet (A) has clearly defined grids and so is much easier than this one (B) which is a real challenge. In sheet B the sizes of the grids are more ambiguous and which may, therefore, have more than one answer. Squared paper is useful in investigating these.
At the end of the lesson learners should be asked to say what makes the different patterns. The factors of the grid number should be discussed and also the idea of one more than and one less than. It is possible here to introduce or practise using a letter to stand for "any number".
You could also discuss what makes an interesting all-over pattern.
Key questions
What kind of pattern do you think you are going to get?
Which tables will make vertical lines?
Why do you think this is?
Which tables will make diagonal lines?
Why do you think this is?
What kind of grid do you need to make a pattern of checks?
What do you think makes an interesting all-over pattern?
Possible extension
If they finish early learners could make some similar "puzzles" on different grids for others to do.
Those who are really confident with the grids up to ten could predict what they will get and then explore eleven and twelve grids (which can be drawn on squared paper). They could also be expected to express their findings in algebraic terms where possible.