Copyright © University of Cambridge. All rights reserved.
'Partly Painted Cube' printed from https://nrich.maths.org/
Show menu
Well done to Rajeev from Fair Field Junior School who sent us this solution:
Jo noticed that when she painted some of the faces of her cube then $45$ faces had no paint on them. Her cube was $5 \times 5 \times 5$, and $4$ faces were painted, so $80$ cubes had paint on them and $45$ cubes were unpainted.
Here is a table showing the number of painted cubes for different sizes of cube and numbers of faces painted:
|
Dimensions of
Cube
|
Number of
Cubes
|
1 face
painted
|
2 opposite
faces painted
|
3 faces
painted
|
4 faces
painted
|
5 faces
painted
|
6 faces
painted
|
| $2\times2\times2$ | $8$ | $4$ | $8$ | $8$ | $8$ | $8$ | $8$ |
| $3\times3\times3$ | $27$ | $9$ | $18$ | $21$ | $24$ | $25$ | $26$ |
|
$4\times4\times4$
|
$64$ | $16$ | $32$ | $40$ | $48$ | $52$ | $56$ |
| $5\times5\times5$ | $125$ | $25$ | $50$ | $65$ | $80$ | $89$ | $98$ |
| $6\times6\times6$ | $216$ | $36$ | $72$ | $96$ | $120$ | $136$ | $152$ |
| $17\times17\times17$ | $4913$ | $289$ | $578$ | $833$ | $1088$ | $1313$ | $1538$ |
| $n \times n \times n$ | $n^3$ | $n^2$ | $2n^2$ | $3n^2-2n$ | $4n^2-4n$ | $5n^2-8n+4$ | $6n^2-12n+8$ |
When Jo had to paint the 2nd face she painted the opposite face. I noticed that it does make a difference in what pattern the faces are painted. The above table applies when painting the second face the one opposite the painted face is painted and after that then you can paint the other faces in any order. Another way to do it is to paint the adjacent face- so after painting the 1st face(say right side) you paint the 2nd face adjacent to it and the 3rd face (say top face)painted must be touching the two painted faces and the 4th face (say bottom face) and the 5th face any remaining side.
Rajeev highlights the idea that painting faces in a different arrangment affects the number of painted cubes. Here is a table with all possible arrangements.
When faces of a larger cube are painted then the number of unpainted cubes depends upon whether the opposite or the adjacent face was painted when painting the second face. Jo's 2nd face was the opposite face so when she painted the 4th face she had $45$ unpainted cubes. If Jo had started painting the adjacent face then she would have been left with $48$ cubes in a $5\times5\times5$ cube.
There is more than one way to end up with any number of cubes - you can end up with $27$ unpainted faces when you paint three adjacent faces in a $4\times4\times4$ cube and also in a $5\times5\times5$ cube when you paint all $6$ faces.
Another way to think about this problem is to imagine removing all the painted cubes and leaving behind a cuboid each time. What can you say about the difference between the largest and smallest dimension of such a cuboid?
Elizabeth, a teacher at Rutherford College, New Zealand, has sent us this very nice diagram that demonstrates visually what happens when you remove a number of faces from an $n \times n \times n$ cube.
Write $N$ for the number of unpainted cubes remaining.
The first thing to notice is that when we remove the painted faces, we will always be left with an unpainted cuboid.
When one face i
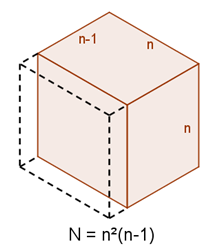 s painted, we are left with an $n \times n \times (n-1)$ unpainted cuboid. The diagram below shows the case when the front-left face has been painted:
s painted, we are left with an $n \times n \times (n-1)$ unpainted cuboid. The diagram below shows the case when the front-left face has been painted:Ther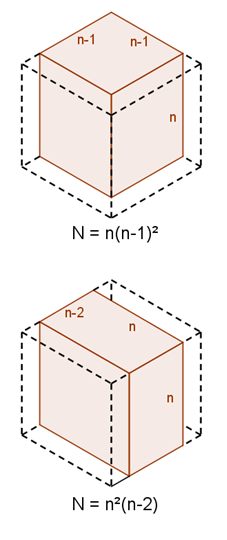 e are two different ways to paint two faces of the cube. These can either be two adjacent faces, or two opposite faces.
e are two different ways to paint two faces of the cube. These can either be two adjacent faces, or two opposite faces.
When the two adjacent faces are painted, we are left with a $n \times (n-1) \times (n-1)$ unpainted cuboid. The diagram to the right shows what happens when the front-left and front-right faces are painted.
 e are two different ways to paint two faces of the cube. These can either be two adjacent faces, or two opposite faces.
e are two different ways to paint two faces of the cube. These can either be two adjacent faces, or two opposite faces.When the two adjacent faces are painted, we are left with a $n \times (n-1) \times (n-1)$ unpainted cuboid. The diagram to the right shows what happens when the front-left and front-right faces are painted.
When two opposite faces are painted, we are left with an $n \times n \times (n-2)$ unpainted cuboid. The diagram to the right shows what happens when the front-left and back-right faces are painted.
When three fac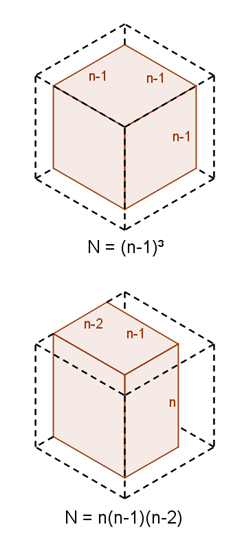 es are painted, there are again two options. The faces can either be those that meet at a particular vertex, or can consist of two opposite faces and one other face.
es are painted, there are again two options. The faces can either be those that meet at a particular vertex, or can consist of two opposite faces and one other face.
If the painted faces meet at a vertex, we are left with an $(n-1) \times (n-1) \times (n-1)$ unpainted cube. The diagram to the right shows what happens when we remove the front-left, front-right and top faces.
If there are two opposite faces painted (and one other), then we are left with an $n \times (n-1) \times (n-2)$ unpainted cuboid. The diagram to the right shows what happens when we remove the front-left, front-right and back-right faces.
 es are painted, there are again two options. The faces can either be those that meet at a particular vertex, or can consist of two opposite faces and one other face.
es are painted, there are again two options. The faces can either be those that meet at a particular vertex, or can consist of two opposite faces and one other face.If the painted faces meet at a vertex, we are left with an $(n-1) \times (n-1) \times (n-1)$ unpainted cube. The diagram to the right shows what happens when we remove the front-left, front-right and top faces.
If there are two opposite faces painted (and one other), then we are left with an $n \times (n-1) \times (n-2)$ unpainted cuboid. The diagram to the right shows what happens when we remove the front-left, front-right and back-right faces.
When there are four faces painted, there are two possible configuations again. The unpainted faces must either be adjacent or opposite.
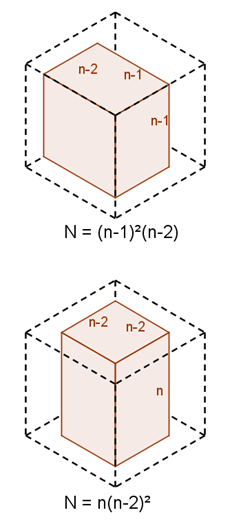
If the unpainted faces are adjacent, then we are left with an $ (n-1) \times (n-1) \times (n-2)$ unpainted cuboid. The diagram to the right shows what happens when the front-left, front-right, back-right and top faces are removed.
If the unpainted faces are opposite, so that the painted faces form a ring shape, then we are left with an $n \times (n-2) \times (n-2)$ unpainted cuboid. The diagram to the right shows what happens when the front-left, front-right, back-left and back-right faces are removed.
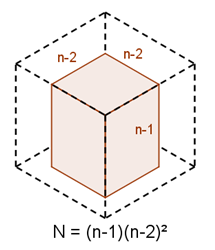
If five faces are removed, there is only one possible configuration, in which we are left with an $ (n-1) \times (n-1) \times (n-2)$ unpainted cuboid. The diagram to the right shows what happens when only the bottom face is unpainted.
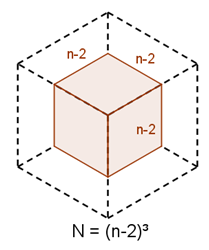
When all six faces are painted, so all are removed, what remains is a cube of side-length $n-2$, as shown in the diagram to the right.
This demonstrates that the number of unpainted cubes can always be written as the product of three factors which differ from each other by no more than $2$.
We can use this to see how we can leave $45$ cubes unpainted. Since $45 = 5 \times 3 \times 3$, we can write this as $45 = 5 \times \left( 5-2 \right) \times \left( 5-2 \right)$. This means we can start with a $5 \times 5 \times 5$ cube, and then paint two pairs of opposite faces to leave $45$ unpainted cubes.
This also explains why we cannot leave exactly $50$ cubes unpainted. For this to be possible, we would have to find three numbers that multiplied to give $50$ but differed by no more than $2$. This is impossible:
$50 = 2 \times 5^2$, as a product of prime factors.
We can write $50$ as the product of three positive integers as $2 \times 5 \times 5$, or if one of the integers is $1$, one of the others will have to be at least $5$.
Both of these cases have differences of more than $2$, so we cannot leave $50$ unpainted cubes.