Partly Painted Cube

'Partly Painted Cube' printed from https://nrich.maths.org/

Show menu

Jo made a cube from some smaller cubes. She painted some of the faces of the large cube, and then took it apart again.
She counted her cubes and noticed that 45 cubes had no paint on them at all.

Can you work out how many small cubes Jo used to make her large cube, and which faces she painted?

Dan made a cube the same size as Jo's large cube, and also painted some of the faces.

How many unpainted cubes might Dan have ended up with?

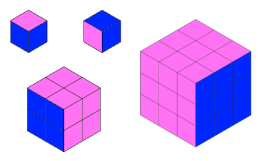
Now explore the number of unpainted cubes for some other sizes of cube. Here are some questions you might like to consider:

If the number of small cubes along each edge is $n$, can you find expressions for the number of unpainted cubes when you paint 1, 2, 3, 4... faces?
The number of unpainted cubes can always be expressed as the product of three factors. What can you say about these factors?
There is only one way to end up with 45 unpainted cubes. Are there any numbers of cubes you could end up with in more than one way?
How can you convince yourself that it is impossible to end up with 50 unpainted cubes?

Click here for a poster of this problem