 Links to the NRICH website Home page
Links to the NRICH website Home page

30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Published 2010
2010: A Year of Investigations
Some activities built around $10$ and $2010$
Here's a list I've been compiling annually for donkeys' years. I've offered it to students, to teachers in LA schools and independents, to those in primary and middle schools, and to teachers in disadvantaged schools in South Africa.
Time, Distance, Measurement
How long is $2010$ seconds?
How long is $2010$ minutes?
How many lots of $2010$ seconds/minutes will there be in $2010$?
How long does it take you to walk $2010$ paces? How many times do you have to walk $2010$ paces to get to school?
How far is $2010$m? How far is $2010$cm? How far is $2010$mm?
Are you $2010$cm tall? Do you know anyone who is $2010$cm tall?
Can you run $2010$cm? How long does it take? How long do you think it will take you to run $2010$m? Try it and see if you're right.
Your class decides to run a relay race. The total distance is $2010$m and everyone runs an equal share. How far does each person have to run?
How long does it take you to do $10$ step-ups? If you start on January 1st and do $10$ step-ups every day when will you have done $2010$?
How well can you estimate $10$cm? $10$m? $10$g? $10$kg? $10$ml? $10$ seconds? $10$ minutes?
If you drink a cup of tea every day how old will you be when you've drunk $2010$?
Do you drink $2010$ml in a day?
How many buckets do you think $2010$ cups of water would fill?
How much is $2010$ litres? Do you need $2010$ litres to wash your hands/to have a bath/to flush the toilet/to have a swim?
If you persuade your parents to give you $1$p pocket money on January 1st, $2$p on January 2nd, $3$p on January 3rd, $4$p on January 4th, $5$p on January 5th ... will you get a total of $2010$p pocket money in January?
If you persuade your parents to give you $1$p pocket money on January 1st, $2$p on January 2nd, $4$p on January 3rd, $8$p on January 4th, $16$p on January 5th ... will you get a total of $2010$p pocket money in January? Will there be a day when they will have to give you £$2010$?
Dates
October 10th will be $10$/$10$/$10$. When will a date like this next happen? How many dates like this can you find? How old will you be on each date?
August 6th will be $6$/$8$/$10$. How many dates in $2010$ can you find where the three numbers go up in a regular sequence?
April 6th will be $6$/$4$/$10$. How many days will there be in $2010$ when the third number is the sum of the first two?
November 21st will be $21$/$11$/$10$. How many days will there be in $2010$ when one number is the difference of the other two?
May 2nd will be $2$/$5$/$10$. How many days will there be in $2010$ when the third number is the product of the first two?
(Today's Date - $01$/$06$/$2009$ is an example of this kind of problem on NRICH.)
Collections
What would $2010$ seeds, or beans, or grains of rice, look like? Would they fill a matchbox? Would they cover a plate? Would they cover a sheet of newspaper?
What would $2010$ bottle tops look like? How many of them could you pick up in one hand? If you put them all in a bag could you lift them? If you lay them all out how far will they stretch? How good a circle could you make with them? How many people could stand inside the circle?
What about $2010$ $1$p coins?
Games
Invent a game played with $10$ matchsticks.
Invent a game for $10$ people.
Invent a game where you have to do $10$ things.
Invent a game using a set of cards numbered from $1$ to $10$.
$10$ teams take part in a football competition. Each team plays a game against each other team. How many games are played altogether? How many games would be needed if they are playing a knock-out competition?
I think of a number between $1$ and $2010$. How many tries do you need to guess it?
Decagons
How well can you draw a regular decagon freehand? Do you get better with practice?
Can you construct a perfect regular decagon?
Draw a regular decagon and all its diagonals. How many diagonals are there? What shapes can you find in the diagram? Can you find any sets of parallel lines? Can you find any sets of perpendicular lines?
Draw two lines across a regular decagon. What shapes do you get? Cut the decagon along these lines. What shapes can you make by fitting them together in different ways?
Patterns and designs
Make a design based upon decagons. Can you make a design based on decagons with different sizes?
Make the digits of $2010$ on a grid of squares, for example:
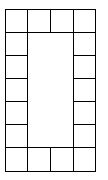
How many squares do you need? Make each digit twice as tall. Make each digit twice as wide. Do both at the same time. How many many squares do you need?
Reflections and rotations
Draw the digits for $2010$ on squared paper again. If you turn each digit upside down they look the same. Will that still be true in $2011$? In $2012$? In $2013$?
Can you find some two-digit numbers whose value stays the same if you turn them upside down? What about three-digit numbers?
Which single digits have lines of symmetry? Which have rotational symmetry?
Which two-digit numbers have lines of symmetry? Which have rotational symmetry?
Can you find some two-digit numbers whose value is unchanged when you reflect them?
Numbers
How long will it take you to count up to $2010$? Perhaps it would be quicker to count in $2$s, or $5$s, or $10$s.
Count backwards from $2010$ (don't try to go too far - but can you manage the tricky bits?).
Write down four numbers that add up to $2010$. What is the easiest set you can think of? What is the most difficult set? Can you find a set where two of the numbers are the same? Can you find a set where three of the numbers are the same? Can you find a set where all four of the numbers are the same?
Some more sets of four numbers which add up to $2010$: find a set where the numbers have fractions. Find a set where the numbers have decimals. (Find a set where the numbers have negative numbers.)
Can you make $2010$ by multiplying two numbers? How many ways to do this can you find?
The answer is $10$. What was the question?
Decimals etc
I'm thinking of a number between $0$ and $0.1$. How many tries do you need to guess it?
Can you put these numbers in order: $0.1$, $0.23$, $0.07$, $0.15$, $0.051$?
How big is a decimetre? How big is a decigram? How big is a decilitre?
Words etc
What does decimate mean? What is a decathlon? What is a decapod? What is a decibel?
What is the tenth month of the year called?
Can you find ways of completing this list of ten words? Here are three to get you started: centimetre, background, television ...