Related Collections

You may also like

problem icon

Turning the Place Over

As part of Liverpool08 European Capital of Culture there were a huge number of events and displays. One of the art installations was called "Turning the Place Over". Can you find our how it works?

problem icon

Where Art and Maths Combine

In this article, Rachel Melrose describes what happens when she mixed mathematics with art.

problem icon

Colouring Curves Game

In this game, try not to colour two adjacent regions the same colour. Can you work out a strategy?

Drawing Celtic Knots

Stage: 3 Challenge Level: Challenge Level:2 Challenge Level:2

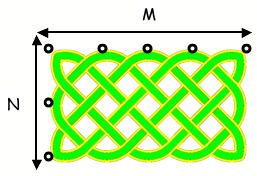
William from Barnton Community Primary School discovered that:


If there is a rectangular Celtic knot that is M by N then the number of ribbons is the highest common factor of M and N.


In this case M = 5 and N = 3 so the number of ribbons is 1.

celtic knot

Therefore, if a square Celtic knot has side length x, the number of different ribbons will be x.

In this case x = 4 so the number of ribbons is 4.

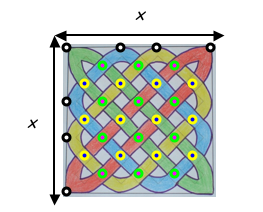
celtic knot

The number of crossovers for a square Celtic knot is $$2x^2 - 2x$$ or $$2x (x - 1)$$

Students from Garden International School also worked on this problem. Here is what Kenn, Jong Woong, Jayme and Marana sent us.
The NRICH Project aims to enrich the mathematical experiences of all learners. To support this aim, members of the NRICH team work in a wide range of capacities, including providing professional development for teachers wishing to embed rich mathematical tasks into everyday classroom practice. More information on many of our other activities can be found here.
Copyright © 1997 - 2012. University of Cambridge. All rights reserved.
NRICH is part of the family of activities in the Millennium Mathematics Project.