 Links to the NRICH website Home page
Links to the NRICH website Home page

30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Expanding Pattern



- Problem
- Solutions
Answer: 92 squares
Building the tenth pattern in rectangles
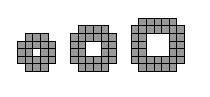 ...
... 
Total 23$\times$4 = 92 squares
Building the tenth pattern from a larger square

Each large square has the centre and corners removed
14$^2-$ 10$^2-$ 4 = 196 $-$ 100 $-$ 4 = 92
Using smaller rectangles and algebra
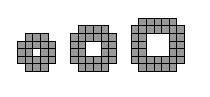
Break the pattern down into four rectangles, each two squares wide, and four L-shaped corner pieces, of three squares each.
Pattern 1 = $4 \times 2 \times 1 + 4 \times 3 = 20$
Pattern 2 = $4 \times 2 \times 2 + 4 \times 3 = 28$
Pattern 3 = $4 \times 2 \times 3 + 4 \times 3 = 36$
Pattern n = $4 \times 2 \times n + 4 \times 3 = 8n +12$
Pattern 10 = $4 \times 2 \times 10 + 4 \times 3 = 92$ squares
Using larger squares and algebra
Imagine a large square with corners removed, and a square removed from the middle:
Pattern 1 = $5^2 - 4 - 1^2 = 20$
Pattern 2 = $6^2 - 4 - 2^2 = 28$
Pattern 3 = $7^2 - 4 - 3^2 = 36$
Pattern n = $(n+4)^2 - 4 - n^2 = 8n +12$
Pattern 10 = $14^2 - 4 - 10^2 = 92$ squares