Copyright © University of Cambridge. All rights reserved.
'Crazy Shading' printed from https://nrich.maths.org/
Show menu
Answer: 1:4
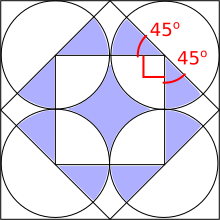

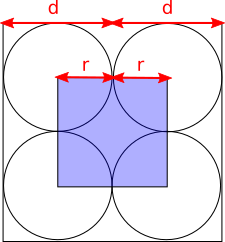
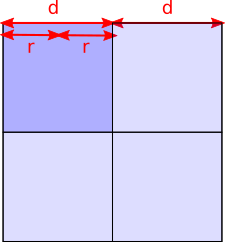
This problem is taken from the UKMT Mathematical Challenges.
You can find more short problems, arranged by curriculum topic, in our short problems collection.