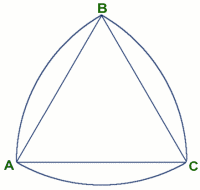
The triangle ABC is equilateral. The arc AB has centre C , the arc BC has centre A , the arc CA has centre B and all three arcs have the same radius equal in length to the sides of the triangle.

Imagine a roller that has this cross-section. Place it on the floor and lay a plank of wood across it. Try to push the plank horizontally on the roller. What happens and why?

Though the animation shows the rolling triangle contained in a box, we are asking you to describe what happens when it rolls along the floor with a plank of wood on top of it..

See also the Coke Machine problem. This relates to the 50 pence piece which is a seven sided rouleaux (rolling) figure, based on a regular septagon.

CHRISTMAS DECORATIONS

If you make lots of these rolling triangles from old greetings cards and score them along the edges of the equilateral triangles you can make the regular solids (a tetrahedron, an octahedron and an icosahedron) by sticking the flaps together. They look good with the flaps projecting outwards and they are easy to make. You can also make a dodecahedron using 12 rolling pentagons. A rolling pentagon is made in a similar way starting with a regular pentagon.