Kangaroo subtraction

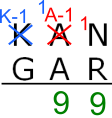
Answer: KAN = 864 (and GAR = 765, OO = 99)

Using column subtraction

Image

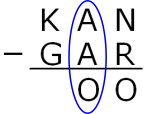
A $-$ A = zero but O shouldn't be zero, so there must have been 'borrowing'/'regrouping'



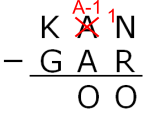
In $^1$A-1, 1 is the tens digit

A-1 is the units digit

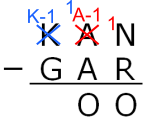
(10 + (A-1)) $-$ A = O so O = 9

 

Image

 

K$-$1 = G

$^1$N $-$ R = 9 means 10 + N $-$ R = 9 so R = N + 1

Largest possible KAN:

9 is taken so let K = 8 $\Rightarrow$ G = 7

A = 6

If N = 5 then R = 6 but 6 is taken

So N = 4 and R = 5

KAN = 864

Using algebra and logic

The difference between '$KAN$' and '$GAR$' is less than $100$ and since $K\neq G$ we must have $K=G+1$.

Next we must have $N < R$ else the difference between '$KAN$' and '$GAR$' would be at least $100$.

Let $R=N+x$ where $1< x< 9$. Then $OO=100-x$ and hence $O=9$ and $R=N+1$. Also we must have $K\leq 8$.

We want the largest value for $KAN$ so we try $K=8$. This forces $G=7$, hence must have $A\leq 6$. Set $A=6$, this forces $R\leq 5$ and hence $N\leq 4$ since $R=N+1$.

So $864$ is the largest possible value for $KAN$, and we have $864-765=99$.