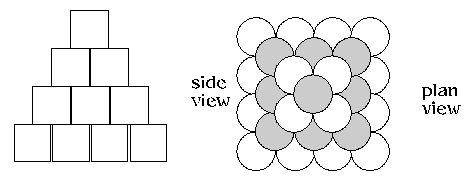
Scott Lewington, age 11, Lea Manor High School and Ling Xiang Ning, Allan, age 12, Raffles Institution, Singapore solved the Human Food problem.

They found square based pyramids with the same number of cans as one triangular stack with a depth of one can (a triangular number of cans) and then three triangular stacks to make up of the same number of cans altogether.

The triangular numbers are: 1, 3, 6, 10, 15, 21, 28, 36, 45, 55, 66, 78, 91, 105,...

The square based pyramid numbers are: 1, 5, 14, 30, 55, 91, 140, 208,...

As we can see, there are two numbers that appear in both lists, 55 and 91. This means that both of them are possible to be a square pyramid (with a 5 by 5 base or a 6 by 6 base) and a triangular stack (with a base of 10 or of 13). Now, we just have to find the three triangular stacks 55 and 91 cans can be made into.

For 55 cans, it could be made into triangular stacks of 6, 21 and 28 (T ₃ + T ₆ + T ₇ ).

For 91 cans, it could be made into triangular stacks of 10, 15 and 66 (T ₄ + T ₅ + T ₁₁ ) or of 3, 10 and 78 (T ₂ + T ₄ + T ₁₂ ) or of 15, 21 and 55 (T ₅ + T ₆ + T ₁₀ ) or 10, 36 and 45 (T ₄ +T ₈ + T ₉ ).

There are other possible solutions. This type of investigation can best be pursued using a spreadsheet with formulae for the different types of patterned numbers in different columns. This leads to conjectures about the algebraic relationships between different patterned numbers which may be proved algebraically.