Three four five

As shown in the diagram, two semi-circles (each of radius $ 1/2 $) touch each other, and a semi-circle of radius 1 touches both of them. Find the radius of the circle which touches all three semi-circles, and find a 3-4-5 triangle in the diagram.

Christiane Eaves, The Mount School, York (Year 10) sent the following solution.

Join the two centres together and drop a perpendicular from the centre of the top circle. The line joining the centres will pass through the point of contact of the two circles because the common tangent at this point will meet both radii at right-angles.

Image

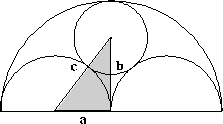
The 3-4-5 triangle is shaded.

Now

$\begin{eqnarray} \\ a &=& \frac{1}{2}\\ b &=& 1-r\\ c &=& \frac{1}{2} + r. \end{eqnarray}$ So, since $a^2 + b^2 = c^2$ then $b^2 = c^2 - a^2$ and

$\begin{eqnarray} \\ b^2 &=& (\frac{1}{2} + r)^2 - (\frac{1}{2})^2 \\ &=& \frac{1}{4} + r + r^2 - \frac{1}{4}\\ &=& r + r^2. \end{eqnarray}$

$ \begin{eqnarray} \\ (1 - r)^2 &=& r + r^2 \\ 1 - 2r + r^2 &=& r + r^2 \\ 1 &=& 3r \\ r &=& \frac{1}{3} \end{eqnarray}$

So $a = {1\over 2}$, $b={2\over 3}$ and $c = {5\over 6}$, or $a = {3\over 6}$, $b={4\over 6}$ and $c = {5\over 6}$. From this it can be seen that the triangle's sides are in the ratio 3:4:5.