 Links to the NRICH website Home page
Links to the NRICH website Home page

30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Diminishing Returns



- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
Navjot from Sherborne Qatar and Siddhant from Singapore International School in India described the pattern in slightly different ways.
Siddhant said: The pattern is made by joining the midpoint of the sides of the smallest square in the image, to create a smaller square. Each odd square is coloured pink and each even square is coloured blue.
Navjot said: The first image shows a pink square, in which there is a blue square rotated by 45 degrees, within which there is another pink square, rotated back to its original position, and this pattern is repeated for a few more squares. The pattern would continue in a similar fashion forever (although some may think that it will stop once we run out of space,
however this is not going to happen because there is always going to be a smaller and smaller area available for another square).
To find the proportion of the total area of the square that is taken up by the small square in the middle, Deana from from KIS International School in Thailand used a beautifully simple method:
1:64
If the smallest pink square area is 1, then the smallest 4 triangles are 1
too. Because the 4 smallest triangles=1 smallest pink square.
And so you need to double the area to 2, then you continue double it for 7
times.
First
1
2
4
8
16
32
64
And you are done!!!
Siddhant and Navjot both found this area using Pythagoras' Theorem.
This is Siddhant's work:
 To solve this, we can make use of simple algebra. If we consider one side of the square as $x$, the total area of that square would be $x^2.$ To find the area of the second largest square, we can use the Pythagoras theorem ($a^2+ b^2 = c^2$), as we can take $c$ as the length of the side of
the square. We can infer that $a$ and $b$ are equal to $\frac x2$, as they are both half of the side of the largest square.
To solve this, we can make use of simple algebra. If we consider one side of the square as $x$, the total area of that square would be $x^2.$ To find the area of the second largest square, we can use the Pythagoras theorem ($a^2+ b^2 = c^2$), as we can take $c$ as the length of the side of
the square. We can infer that $a$ and $b$ are equal to $\frac x2$, as they are both half of the side of the largest square.
Once we calculate this, we see that the area is $\frac{x^2}2$ (since $$\left(\frac x2\right)^2+\left(\frac x2\right)^2=c^2\\
\Rightarrow \frac{x^2}4 + \frac{x^2}4=c^2\\
\Rightarrow \frac {x^2}2 = c^2$$ which is the area of the square with side length $c$.)
We can continue to do this to find the area of the third largest square, which will be $\frac{x^2}4.$ When we look at the pattern forming, we can see that the area is getting halved each time. Hence the total areas for each of the squares will be: $$x^2, \frac{x^2}2, \frac{x^2}4, \frac{x^2}8, \frac{x^2}{16}, \frac{x^2}{32}\text{ and }\frac{x^2}{64}$$
The smallest square in the middle has an area of $\frac{x^2}{64}$. Hence the proportion of the total area that is taken by the smallest square in the middle is $1:64,$ or it takes up a $64^\text{th}$ of the total area of the square.
Bondy, Johanson, Chane, Jeremy and Matthew from Hsinchu International Academy in Taiwan drew some extra lines into the diagram to help them find the areas. Then, they used a spreadsheet to explore what happens. Here is some of their work (you can see their whole presentation here):
At first, we found that the sum of the four outer triangles was $\frac14,$ the next four was $\frac1{4^2}, $ then $\frac1{4^3}$ and so on. We continued this pattern and added all the fractions together.
At first, we tried to use a calculator but it took forever, so we used another methog to solve this problem: Google sheets!
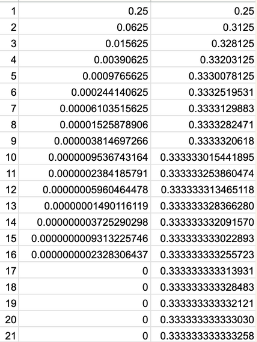
When we added all the fractions together, the sum was equal to $\frac13.$
Yoram from Avenue Primary School in the UK and from Allenmoos School in Switzerland had a very simple explanation for what proportion of the square would be blue if the pattern continued forever:
The blue part is one third. Because the largest four blue triangles make two of the biggest pink triangles. And it is the same all again with the smaller triangles.
And so, pink is twice as much as blue.
Niharika from Leicester High School for Girls used a similar idea, but with slightly more explanation. Click here to see Niharika's work.
Navjot and Siddhant both investigated the sequences formed by the areas. This is Siddhant's work:
I first tried finding the proportion of blue at each stage of forming the image (using the interactive feature). For example, at the 0th stage, the proportion of blue in the image would be zero. In the first stage (i.e when the first blue square is formed), the proportion of blue would be $\frac12$ of the total image as the area of that blue square is $\frac{x^2}2.$ However, I realized that the
proportion of blue decreases with the addition of every new pink square, and hence I had to subtract the area of the new square from the proportion of blue. Whenever a new blue square is added, we must add the area of that square to the proportion of blue that existed in the previous stage. The structure of the pattern then became: $$0, \tfrac12, \tfrac12 - \tfrac14, \left(\tfrac12 -
\tfrac14\right) + \tfrac18, ...$$
We can infer that the previous value of the pattern is always [having a particular number] subtracted or added. This number is always $\frac14,\frac18, \frac1{16}, ...$ Therefore we can see the number being added or subtracted is always increasing in the negative powers of $2.$
However, the negative powers of $2$ are either being added OR subtracted. To represent this each time, we can use $\left(-1\right)^n.$
When we add all these elements to generalize the proportion of blue at each stage, we get: $$T(n-1) + (-1)^{t-1} \times (2)^{-t}$$
Where $t$ is the term or stage of the pattern
[$T(n)$ is the proportion that is blue at this stage.]
Let's see if this works:
For the first stage, where $t = 1$, $T(n - 1 )= 0$
$0 + (-1)^0 \times 2^{-1} =1 \times \frac12 =\frac12$
For the second stage, where $t = 2, T(n-1) = \frac12$
$\frac12 + (-1)^1 \times 2^{-2} =\frac 12 -(1) \times \left(\frac14\right) =\frac12 -\frac14 =\frac14$
For the third stage, where $t = 3, T(n-1) = \frac14$
$\frac14 + (-1)^2 \times 2^{-3} =\frac14 + (1)\left(\frac18\right) =\frac 14 + \frac18 =\frac 38$
Therefore, this formula works and shows the correct proportion of blue at each stage of the formation of the image.
Navjot used some definitions and formulae to find the blue area. Navjot got the same sequence as Siddhant for the area of the blue parts at different stages: $$0,\tfrac12,\tfrac12-\tfrac14, \tfrac12-\tfrac14+\tfrac18, ...$$
Navjot wrote a general term as: $$\tfrac12-\tfrac14+\tfrac18-\tfrac1{16}+\tfrac1{32}-\tfrac1{64} ...$$
And wrote:
This can be simplified to: $$\left(\tfrac24-\tfrac14\right) + \left(\tfrac2{16}-\tfrac1{16}\right) + \left(\tfrac 2{64}-\tfrac1{64}\right) + ”¦$$
Which can be finally simplified to: $$\tfrac14 + \tfrac1{16} + \tfrac1{64} + ”¦$$
The sequence seems to be in the pattern of $\left(\frac14\right)^n$ where $n\ge1.$
Now, we can finally add all these areas up to infinity and that will give us the area of the blue squares, and the fraction of the large square that is blue.
$\sum\left(\frac14\right)^n$, Starting from $n=1$ [and up] to infinity.
Formula of a geometric sequence going up to infinity is $ a\left(\frac1{1-r}\right),$ where $a$ is the first term of the series and $r$ is the common ratio.
Therefore, the series sums up to $$\left(\tfrac14\right)\times\left(\tfrac1{1-\tfrac14}\right) = \left(\tfrac14\right)\times\left(\tfrac1{\frac34}\right) = \left(\tfrac14\right)\times\left(\tfrac43\right) = \tfrac13$$
So, a third of the large square is blue.
For each of the images below, it is possible to find the fraction that is blue using a simple argument like Yoram's or Nihanika's. It is also possible to find the area of each blue shape using a doubling method like Deana's, or by drawing smaller squares inside the square.
Bondy, Johanson, Chane, Jeremy and Matthew used diagrams and spreadsheets again. Here is some of their work (you can see their whole presentation here):
 At first, we found that the largest triangle was half the area of the square. The second largest was $\frac18,$ the third largest was $\frac1{32}$ and so on. We can write the sum of these fractions as
$$\tfrac12+\left(\tfrac12\times\tfrac14\right)+\left(\tfrac12\times\tfrac14\times\tfrac14\right)...$$
At first, we found that the largest triangle was half the area of the square. The second largest was $\frac18,$ the third largest was $\frac1{32}$ and so on. We can write the sum of these fractions as
$$\tfrac12+\left(\tfrac12\times\tfrac14\right)+\left(\tfrac12\times\tfrac14\times\tfrac14\right)...$$
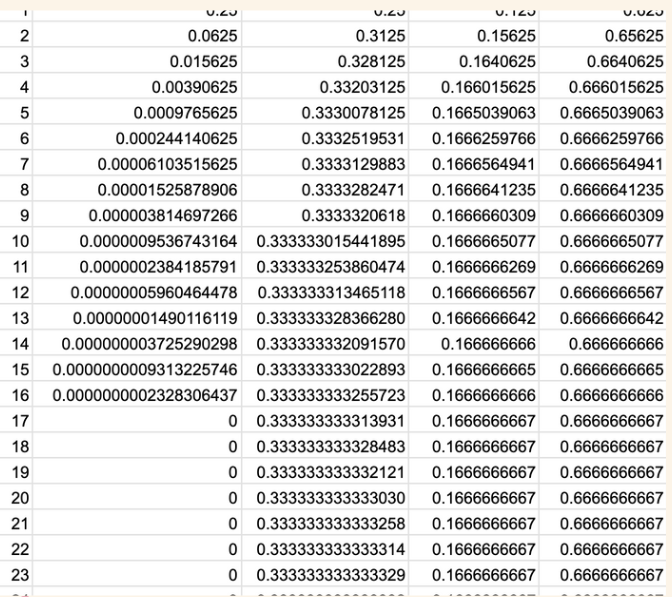
We used Excel to estimate the sum, and found that it is approximately equal to $0.\dot6,$ which is $\frac23.$
Note that this uses the calculations from the first pattern (shown above). The sums are halved in the third column, and then in the fourth, $\frac12$ is added to each one.
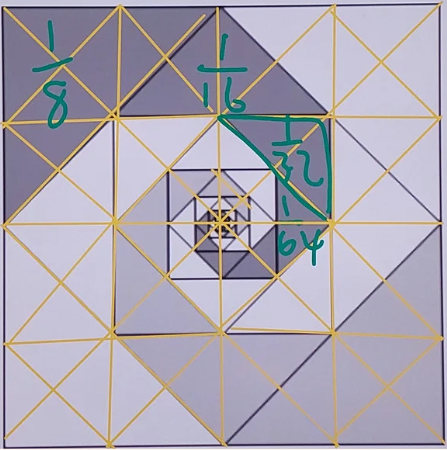
At first, we saw the design could be split into four congruent spiral shapes - one dark gray, one light gray and two white. If we just want to find the area of the dark gray one, we know that $1\div4$ will be $\frac14.$ We checked our answer in Excel by adding the areas of the triangles.
Note that the numbers in the first column are ($\frac12, \frac14$ - not shown), $\frac18, \frac1{16},$ ... . Then the numbers in the second column are these added together, and finally the numbers in the third column are the numbers in the second column, each divided by $4$. Why does this method work?
Navjot found the blue areas using algebra, Pythagoras' Theorem and formulae for geometric sequences:
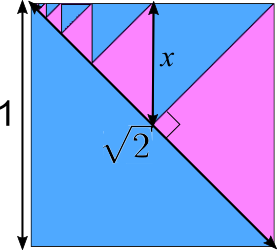
In this diagram, the largest diagonal goes through the midpoint of the whole square. The other diagonals are perpendicular to this one. The diagonal on the farthest right intersects with the first diagonal at its midpoint.
Let's assume that the side length of the major square is $1,$ therefore the area of the first blue triangle is $\frac12\times1^2=\frac12.$
Since the side length is $1,$ the first diagonal's length is $\sqrt{1+1}=\sqrt2,$ the perpendicular bisector (the diagonal on the farthest right) cuts this diagonal into 2 equal halves, each of length $\frac{\sqrt2} 2.$ Since the bisector and the diagonal meet at the midpoint of the square, we know that the bisector is of the same length. This information will help us in finding the side
length of the second largest triangle. We can use the Pythagorean theorem to find this length. This is made easier by the fact that the triangle is right angled AND isosceles.
So: $\sqrt{2x^2} = \frac{\sqrt2} 2$ so, $x =\frac12$. This means that the 2nd triangle's area is $\frac12\times\left(\frac12\right)^2=\frac18.$
Now, let's forget the rest of the square and let's concentrate on the smaller square with side length $0.5.$ We notice that this pattern is repeated, it's just that the diagonal of the entire square is now $\frac{\sqrt2} 2$ rather than just $\sqrt2.$ This means the new diagonal that is farthest to the right bisects this diagonal of length$\frac{\sqrt2}2,$ halving it into $\frac{\sqrt2}4.$
Repeating the same process again, we notice that the two sides of the pink triangle are of length $\frac{\sqrt2}4$ which means that the smaller blue triangle has a hypotenuse of $\frac{\sqrt2}4.$
Using this information we can find that triangle's side length.
$\sqrt{2x^2}=\frac{\sqrt2}4$ so $x=\frac14$
So the triangle's area is $\frac12\times\left(\frac14\right)^2=\frac1{32}$
So, just looking at the three largest triangles, we can see a pattern in terms of areas, the largest triangle's area is $\frac12,$ the second largest is $\frac18,$ the third largest is $\frac1{32}.$ If we factor the $\frac12$ out and write the remaining fraction in powers of $\frac12,$ the areas are $$\left(\tfrac12\right)\times\left(\tfrac12\right)^0,
\left(\tfrac12\right)\times\left(\tfrac12\right)^2, \left(\tfrac12\right)\times\left(\tfrac12\right)^4, ...$$
The $n^\text{th}$ term of the sequence is $\left(\frac12\right)\times\left(\frac12\right)^{2n}$
So the area of 5 blue triangles would be:
$\sum{\frac12\times\left(\frac12\right)^{2n}}$, from $0$ to $4$ (I used $n=0$ because that would give the value $\frac12\times1,$ which is the area of the first triangle)
$ =\frac12\sum{\left(\frac14\right)^n},$ from $0$ to $4$
$ = \frac12\times\dfrac{1\left(1-\left(\frac14\right)^4\right)}{1-\frac14}$ (Formula for [sum of] geometric sequence up to $k$ terms is $\frac{a(1-r^n)}{1-r}$ where $a$ is the first term of the sequence, [$k$ is the number of terms], and $r$ is the common ratio)
$= \frac{341}{512} = 0.66602$
Carrying this procedure on forever would mean that we use the same series but instead of $4$ being the last $n$ value, we go up to infinity.
Therefore the total blue area now is as follows:
$\sum{\left(\frac12\right)\left(\frac14\right)^n}$ from $n=0$ to infinity
Using the formula used for the first part of the question:
Sum $\frac12\times \dfrac{1}{1-\frac14} = \frac12\times\frac43=\frac23.$
Therefore, if the pattern was infinitely repeated, the $\frac23$ of the area of the square would be blue.
Navjot had a very good idea for a solution to the next shape, but unfortunately it contains a mistake:

For the second diagram, the area covered by blue in this shape must be a quarter of the area of the square in the first part of the question since the structure is very similar, it's just the fact that only 1 of the 4 triangles formed by the outer square and the inner, tilted one were blue.
In fact, this isn't true because only half of the "layers" of squares in the first shape contain blue triangles (and the other half are pink), but every single layer of the second shape contains a blue triangle.
Navjot continued with the next diagram. Again, it would be possible to use a method like Yoram's to calculate the blue area directly, or to split the square into smaller squares to find the area of each blue triangle. Navjot kept using Pythagoras' Theorem:
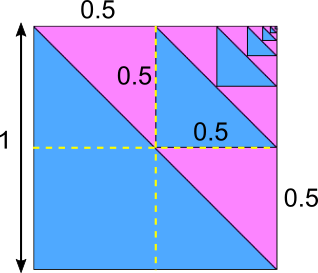
For the third diagram, the idea I will be implementing will be pretty similar to that of the first diagram of this section. Let's again assume that the side of the large square is $1$ unit, therefore the first diagonal that splits the square into a blue triangle and the rest of the shape is
$\sqrt2$ units long. The lines that perpendicularly bisect two of the sides of the square intersect at the mid point of the diagonal.
Since they meet at the midpoint and come are perpendicular to the sides of the square, two right angled isosceles triangles are formed with hypotenuse lengths being $\frac{\sqrt2}2$ units long. Using the Pythagorean theorem:
$\sqrt{2x^2} = \frac{\sqrt2}2$
Therefore, $x = 0.5$
As there are $2$ of these triangles, there are $4$ sides that are $0.5$ units long, $2$ of these create another right angled triangle, which is again isosceles.
Now, like the first square of this part of the question, let's forget about the initial square and zoom into the shape so that we get the original square again, just with side lengths $0.5$ units. By doing this, we are back to the initial part of this question and can repeat what we have
done before.
Since the side length is $0.5$ units this time, the diagonal is $\frac{\sqrt2}2$ units long. And again, like before, there are $2$ lines which are perpendicular to the sides of the square and are meeting at the mid point of the diagonal, halving the diagonal length into $\frac{\sqrt2}4$
To find the length of the straight lines that intersect at the mid point of the diagonal, we use the Pythagorean theorem again:
$\sqrt{2x^2} = \frac{\sqrt2}4$
Therefore, $x = 0.25$
We keep repeating this process again and again until we get the side lengths of our 5 triangles. Doing so, gives us the side lengths $1, \frac12, \frac14 ,\frac18$ and $ \frac1{16}$
So the area of all the blue triangles combined is:
$\frac121^2+\frac12\left(\frac12\right)^2 +\frac12\left(\frac14\right)^2+\frac12\left(\frac18\right)^2+\frac12\left(\frac1{16}\right)^2 = \frac{341}{512}$
If we carry this on infinitely, we get another infinite geometric series:
$\sum{\left(\frac12\right)\left(\frac12\right)^{2n}}$, from $n=0$ to infinity
$=\frac12\sum{\left(\frac14\right)^n}=\left(\frac12\right)\left(\frac43\right)=\frac23$
Therefore, $\frac23$ of the square is shaded blue.
You may also like
Chocolate
There are three tables in a room with blocks of chocolate on each. Where would be the best place for each child in the class to sit if they came in one at a time?
Tweedle Dum and Tweedle Dee
Two brothers were left some money, amounting to an exact number of pounds, to divide between them. DEE undertook the division. "But your heap is larger than mine!" cried DUM...
Sum Equals Product
The sum of the numbers 4 and 1 [1/3] is the same as the product of 4 and 1 [1/3]; that is to say 4 + 1 [1/3] = 4 � 1 [1/3]. What other numbers have the sum equal to the product and can this be so for any whole numbers?