 Links to the NRICH website Home page
Links to the NRICH website Home page

30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Published 2011
CPD Support Using Rich Mathematical Tasks
The introduction of the renewed framework in September 2006 presented a fantastic opportunity to reinvigorate mathematics across primary schools. The emphasis on mathematical processes combined with the messages from Excellence and Enjoyment (2003), encouraging teachers to "take ownership of the curriculum" and to "be creative and innovative in how they teach", could make for a drastic shift in the learning and teaching of mathematics which many of us would welcome. At NRICH, we found ourselves in a potential position to help.
Mathematical thinking and problem solving are at the heart of NRICH, but in the past we have struggled to communicate how our resources might be used in classrooms. We realised that in order to encourage more teachers to change the way they approach mathematics, more support was needed on the NRICH website. This focused on two inter-related developments:
-We have produced curriculum mapping documents which link NRICH activities to framework objectives.
-We are writing more detailed teachers' notes to accompany our resources, suggesting ways of incorporating them into everyday lessons.
When we work directly with teachers, it is relatively easy for us to share our philosophy but we hope that the steps above go some way to help teachers who are remote from us. However, we thought we could do more. We wondered whether it would be possible to offer some form of Continued Professional Development (CPD) through the website.
With this in mind, armed with money from an NCETM grant, we sought schools who would be interested in helping us. Mark Dawes, an AST at Comberton Village College, agreed to take on the venture and he recruited three feeder primary schools. The aims of the project were two-fold:
-To improve mathematics teaching and learning in the schools through the use of rich problem-solving tasks
-To trial and refine a professional development resource, to be available online, which would mediate the use of NRICH and problem-solving materials
(This page gives a brief summary of the project.) I was lucky enough to have the opportunity to go into each school for an afternoon in the autumn term to work with the staff. We did some NRICH problems together and discussed what makes a resource a "rich task". This led into talking about what we as teachers value in mathematics and the kind of "behaviours" we would like to encourage. Do we only praise a pupil who gives the correct answer first? What about the child who takes a little longer but is able to explain his or her thought processes? Having introduced the teachers to the NRICH website and the curriculum mapping documents, each school decided on a particular focus for the year. These included improving how children explain calculations and methods while problem solving, and how they record their investigative work.
During this first term, the participating teachers selected problems from NRICH to use in their mathematics lessons. Mark observed many lessons and also led several. We had set up a wiki to facilitate communication about their experiences and to share resources. What follows is a selection of some of the problems the teachers chose to use in the classroom and their associated comments.
One of the Reception teachers picked out Building with Solid Shapes which invites children to decide which of the buildings below would fall down if they tried to make them. Which ones would be unstable and possibly collapse?
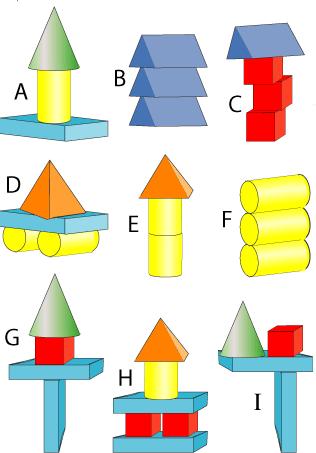
She used this activity as part of a lesson on 3D shapes, which was a fairly new topic for her class. Having started with a few songs which focused on shapes, she introduced them to a cube, cylinder and sphere, and discussed their properties. The children then worked in pairs to identify a shape between them, and they then moved on to the Building with Solid Shapes activity. The teacher wrote on the wiki:
They really enjoyed the activity and were very good at knowing which towers would be easy to build and which ones would fall over. Some children gave excellent reasons why the unstable towers would fall over, "it's not flat", "the edge is pointy", etc ... The children tried to build more stable towers with each set of shapes without any prompting from me. Once the activity had finished most of the group chose to stay on the carpet with the shapes to continue experimenting with which towers are stable/unstable.
Mark was asked to use Domino Sorting with two mixed Reception/Year 1 classes. The problem involves these dominoes taken out of the full set:
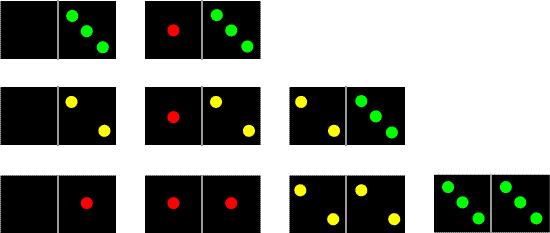
Children are challenged to sort them into two groups in different ways and to justify why some cannot be grouped.
Mark used pre-prepared interactive whiteboard files throughout this lesson which introduced the problem through a series of separate challenges, such as separating the dominoes into three groups, those which have 1 spot, those which have 2 spots and those which have neither (these were called 'problems'). He structured it so that the first question was set up and begun on the carpet using the whiteboard, then pairs worked together on it, then discussion followed back on the carpet and then the second question was posed etc. One of the class teachers commented:
The children were not sitting for long and there were quite a few mathematical concepts covered. They were able to investigate, but also consolidate what they were learning by returning to the carpet each time for a group discussion.
The other said:
The children were able to articulate their ideas well. It was nice to be able to stress that while some classifications have a "problems" group, others don't (e.g. odd/even).
One of the other teachers, of a Year 1/2 class, selected I'm Eight. Here is an edited version of the problem:
When I went into a classroom earlier this week a child rushed up to tell me she was 8 that day! Well, Happy Birthday to everyone who has a birthday today!
If you are 8 then this could be for you, but if it is another number then you just change the 8 to whatever your age is today.
There is not a lot to say to introduce this challenge. It's really just to find a great variety of ways of asking questions which make 8.
Things like 6 + 2, 22 - 14, etc.
But you need to get examples that use all the different mathematical ideas that you know about.
The children had use of cubes and number squares if they wanted them, and they were provided with sheets on which to record their number sentences. These sheets were differentiated in that some had number sentences, which the children had to solve in order to select those that made 8, whereas others just had suggestions for the operations which could be used. This teacher posted the following on the wiki:
The children really enjoyed this activity, which was accessible to all at different levels. The support children liked the thought of being "number investigators", and responded well to the independence of working out the answers for themselves, with cubes. The core groups also responded well, having the security of first completing the number sentences given
before having to think of their own. The extension children saw the activity as a challenge to think of as many differing and difficult number sentences as possible ... few seemed content to write down simple ones when they could think of harder ones for themselves.
Overall, this activity was a great one for a class with such a diverse range of mathematical ability. Everyone felt included at their own level. It was also effective for showing some gaps in the children's knowledge ... which I can use to plan into future teaching.
In the Money was chosen by a Year 4/5 teacher. She prepared a PowerPoint file which contained two challenges, and the children worked in groups using mini-whiteboards. The first of these was the problem taken from the website, the second was a similar question which used different fractions. Mark, who was observing, wrote up a detailed account of the lesson on the wiki which describes how the suggested solutions for the first challenge were collected on the board and the children were asked to explain why each could be an answer. This led to a discussion of the properties of the total number of coins (it must be divisible by 3 and 4) and a consensus of what in fact was a unique solution. The children were then able to tackle the second challenge in their groups. Mark remarked:
The pupils were all engaged in the task and enjoyed it. It was lovely to see them begin with an idea and then change it as they found it didn't work!
As part of a lesson involving several domino activities, another teacher, this time of a Year 5/6 class, chose Amy's Dominoes:
Amy has a box containing domino pieces but she does not think it is a complete set.
She has 24 dominoes in her box and there are 125 spots on them altogether.
Which of her domino pieces are missing?
The teacher asked for feedback from the children and posted this pupil's comment on the wiki:
I think it is a 10/10 game because it was a challenge and quite mathematical. We did our own style of jottings. It was great to do with a partner: I felt more confident talking to somebody. It took a while.

The last example comes from another Year 5/6 class. This teacher used Flashing Lights which involves two lights flashing at the same time, then one of them flashing every 4th second, and the other flashing every 5th second. The question asks how many times they flash together during a whole minute and then goes on to look at three lights.
This was not a very difficult investigation for some children, but the hard part was recording their findings (this is the focus of our work). Many children were able to record numerically what had happened but could not explain it in words. Most children listed multiples and used highlighters to show flashes that coincide - different colours for three lights to show
different combinations flashing together. Others listed every number and highlighted flashes in different colours.
The problem was chosen to introduce common multiples. The teacher began by splitting the class into two groups, one clapping every 3 beats, the other every 6 beats and they talked about when the clapping would coincide. A similar activity followed, with other rhythms and then the context of the lights was introduced. The teacher wrote the following on the wiki:
We had some discussion about whether 0, 20, 40, 60 is four flashes in 1 minute or just three. It was interesting for me to observe the methods adopted by various children, and to note which children were devoid of methods - not necessarily the "less able" ones.
In January 2008, all the teachers from the three primary schools got together for an afternoon. This allowed them to meet each other face-to-face and discuss the successes and difficulties so far, as well as to arrange some inter-school visits. It was also an opportunity for them to critique the CPD documents which we had prepared. As mentioned above, eventually, we want these documents to be a substitute for the input Mark and I had had in person, and to encourage and support teachers in truly embedding rich tasks into their practice. The teachers worked in pairs or small groups to go through the materials and gave us invaluable feedback. This included:
-They liked the practical elements, which made them reflect on important concepts such as a matching activity where problems that promoted higher-order thinking skills were paired with those requiring only lower-order thinking.
-They liked the concrete examples of problems which were worked on as a whole group and then discussed.
-They found some of the materials too theoretical and too much to read. They recognised that this was important but suggested these parts could be supplementary documents.
-They wanted to see video clips available which showed NRICH resources being used in the classroom so that particular issues were exemplified.
Throughout the spring term, the teachers took each other up on offers of visiting each other's classrooms as observers or as team teachers. This opportunity in itself prompted several comments on the wiki, for example:
I found both these visits very interesting and enjoyed watching the ways the children tackled their investigations and talking to them about what they were doing. I shall definitely use both the investigations. The best thing was that I could try the investigation myself and discuss strategies with R, it was great to be a pupil!!
I think this speaks volumes in terms of how important it is that we, as teachers, engage with mathematics ourselves and this remains a key feature of the CPD materials.
One school decided that they wanted to hold an evening for parents to tell them about this "new way" of teaching mathematics. I was privileged to be involved with this event and, in a similar way to the teachers themselves at our first meeting, the parents tackled an NRICH problem. It was fantastic to see them discussing mathematics with each other: conjecturing, explaining, justifying, varying their ideas accordingly, coming to conclusions and generalising. Drawing their attention to the buzz that had taken over the room and the value of their interactions, meant that we could reflect on the fact that we may not have written anything down which was "neat and tidy" but we had been engaging in high-level mathematical thinking. One of the teachers then took the parents through a lesson based on another NRICH problem and shared what the children had talked about and done. The evening seemed to be a good way of getting parents "on board" and helping them to understand the importance of mathematical problem solving.
The comments on the wiki have been a great help to NRICH in several ways. These have ranged from the specific, such as a problem having a different star rating, to the more general, for example asking children to write "handy hint" for anyone else tackling the investigation who couldn't think where to start. One particular thread gave us food for thought:
I feel the investigations are good so far but NRICH should have Smart pages for us to go with rather than having to start from scratch - it's great to share them but could NRICH not be producing these? - otherwise I think teachers will look elsewhere for ready made investigations - just a thought! I don't mind because I am maths coordinator and it's good for me but other teachers do not always have the time I think.
Another teacher chipped in:
I agree - that the investigations are good extensions of our maths teaching but there is a lot of work needed so that all children can access them. I know teachers who visited me asked how long I'd spent producing the Smartboard pages. This work ensures the success of the ideas from NRICH. Having said that the NRICH investigations are providing the children with challenges that use the maths which they have learnt which is what it's all about!! We are happy to share our work but a few more materials provided for us wouldn't go amiss!!
This highlights a dilemma for us at NRICH. I have already said that we are improving the support we give teachers on the site by writing notes to indicate how a particular problem could be used. This often includes making recording or supplementary sheets available to download as pdfs and Word documents. Developing interactive whiteboard files is a different matter, however, for two main reasons. Firstly, we believe that there is value in not being too prescriptive so that teachers are encouraged to engage in a problem themselves and therefore to take some ownership of the way it manifests itself in the classroom. Secondly, on a practical note, were we to provide whiteboard files as a matter of course, we would have to make sure they were available in all formats, compatible with all whiteboards, which we simply do not have the time and expertise to do. We are trying to find a balance, which is not always easy. Many of the teachers involved in this project have given their permission for us to publish the extra resources they have created, for which we are very grateful. In addition, some of their lesson descriptions have informed the notes accompanying the relevant problem.
As a result of the teachers' input, we have also revised the CPD resources quite significantly. Two of the schools allowed us to film lessons in which NRICH problems were used and so clips from these will be incorporated as was suggested. The next stage was to trial these improved versions with another group of schools. You can see the resources here.
I'd like to conclude by thanking all the teachers from the three primary schools, and Mark, for their enthusiasm, dedication and honesty. I know their work will help other teachers to make use of NRICH in the future and I sincerely hope that they feel as if they have benefited from their involvement. I leave you with two comments which I think give us all food for thought:
It has made me think more carefully and creatively about different ways to approach a learning objective.
I found I was discovering things at the same time as the children and getting excited with them (not a bad thing for them to see...!!).
References
DfES (2003) Excellence and Enjoyment A Strategy for Primary Schools
DfES (2006) Primary Framework for Literacy and Mathematics
This article first appeared in Primary Mathematics, published by The Mathematical Association.