- Races
- Board games
- Spatial strategy games
- Numerical strategy games
- Card games
- Arithmetical games
- Matching games
- Mystery games

Clearly these are not necessarily mutually exclusive groupings, but I think they can be helpful nonetheless. So, here are some of my favourite games on NRICH which exemplify some of the different categories listed above. As with all resources on the website, some are interactive (and can therefore be played against the computer or against a friend but on the computer), while others give instructions and therefore might require the preparation of simple materials.

Seeing Squares is a game of spatial strategy and there is an interactive version on NRICH:

Players take it in turns to make a mark on any spot by clicking on it. (The first player makes red marks and the second player or computer makes green marks.)
The winner is the first to have four marks that can be joined by straight lines to form a square. Squares can be any size.
For an extra challenge, why not increase the size of the grid using the arrow buttons?

This game is fantastic at so many different levels. Firstly, it challenges pupils to think carefully about the properties of a square and it addresses the misconception that squares have to have horizontal and vertical sides. At a deeper level, questions can be asked about where might be the best place to start this game. This leads into systematically investigating the number of different squares which can be drawn at each point on the grid. Of course the game is easily made into a practical one away from the computer based simply on a paper grid (perhaps laminated for long-term use) and counters in two different colours.

One of the comments teachers make when I introduce them to Seeing Squares is the fact that it is so simple yet so powerful. The same could be said for the well-known spatial strategy game, Noughts and Crosses. An interactive version (playing against the computer) can be found on the site here.

As you will no doubt know, players take it in turns to mark a square on the grid, one player drawing "noughts" and one "crosses", the aim being to get a line of three. On the website version, you are tantalisingly informed "If you play correctly you never lose and if your opponent plays correctly you cannot win.". This game has great potential for encouraging children to look for all possibilities in a systematic way and in that respect has similarities to the deeper analysis of Square It. However, the analysis here is more accessible, I think, and therefore is a great context in which to promote and focus on clear articulation of a strategy. There are perhaps some unexpected findings, too!

Isomorphic (structurally identical) to Noughts and Crosses is the numerical strategy game, Fifteen:

You take it in turns to choose one of the whole numbers $1$ to $9$ (and each number can only be chosen once). To win you have to pick three numbers that add up to $15$.

One of the appealing things about this game as presented on the website is its ambiguity, I think. Do you stop if, after choosing three numbers, no-one can make $15$? If you carry on, what are the rules for doing so? What happens if you make $15$ using any three numbers you have, or more than three? Indeed, which rules make the "best" game?

You could introduce this game to your pupils without mentioning its similarities to Noughts and Crosses to see whether the children themselves notice. If they need prompting, simply ask the class what Fifteen has in common with Noughts and Crosses and see where this leads. Can this help us to play strategically?

Another set of isomorphic games is the Nim family. Apparently, the word nim is thought to originate from the German word "nimm" which means "take" and this makes a lot of sense once you see how to play. One of the most basic forms of Nim is Nim-$7$:

You will need seven objects, such as counters or blocks. It is a game for two players.
Place the seven counters in a pile or a line and decide who will go first. (In the next game, the other player can have the first turn.)
Each player takes turns to take away either one or two counters.
The player that has the last turn loses.
Keep playing until you work out a winning strategy.
Does it matter who has first turn?
What happens when you start the game with more counters?

Play this a few times, for example you against the class, using counters on the interactive whiteboard, coloured circles stuck to an ordinary whiteboard or overhead counters. This way, the children will get the idea of the game and are also likely to get a small insight into the beginnings of a strategy. What happens when just three counters are left? Challenge them then to play in pairs and to think about how they will beat you.

This game is a great context in which to talk about working backwards, or planning ahead (depending on which way you look at it!), and also provides an opportunity for children to explain carefully how they would win. To encourage a thorough explanation, you could ask one pair to instruct you whilst you play against the rest of the class. Doing exactly what they tell you and seeing whether you win will be a great test of the clarity of their explanation!

As the text of the game suggests, you can take Nim-$7$ to a higher level by introducing more counters. Does it matter whether there is an odd or even number of counters to start with? Can your pupils generalise so that they could explain the strategy whatever the number of counters? This last question to me is the sign of a really good strategy game - knowing how to win even when the game is changed slightly (in this case, by altering the number of counters).

There are many other versions of Nim which can be played with counters, some of which are described here. Got It! is a related game, and also has the property of being generalisable. It is interactive so that you can play against the computer:

Got It! is an adding game for two. You can play against the computer or with a friend.
Start with the Got It! target $23$.
The first player chooses a whole number from $1$ to $4$.
Players take turns to add a whole number from $1$ to $4$ to the running total.
The player who hits the target of $23$ wins the game.
To change the game, choose a new Got It! target or a new range of numbers to add on.

Before reading on, I would encourage you, if you can, to have a go at this game now!

The best way to introduce this game is to challenge the whole class to play against the computer. Don't worry too much to start with about a strategy, just encourage the children to have a few goes and see what happens. More often than not, the computer will win, but this is a great chance to get an insight into the strategy. If the computer makes the total $18$ so that it is the class to go next, what will happen? Why? Identifying what the computer is doing to win is a great way of developing a plan ourselves. If we know we can win when we make $18$, how can we guarantee that we will get to $18$? What would we have to leave the total at on our previous turn?

When I have played this game with children, I often get them to play against me just using a flipchart or ordinary whiteboard rather than the interactivity. I record the numbers that are chosen each time and the running total. Having done this, children can play against each other in pairs just using pencil and paper. This is useful because it gives them a chance to think more about the strategy but also builds up a record of what they have tried. (You may find the Got It Article useful, which asks some probing questions to help you think about the strategy.)

Further generalisations can be made when you change the rules slightly. What if we had numbers $1$, $2$, $3$, $4$ and $5$ with a target of $23$? What would be the strategy to win then? What if we had $1$, $2$, $3$ and $4$ but with a target of $24$? $25$? By clicking on the "Change Settings" button, you can alter both the target and the range of numbers. Many children in the later primary years will be able to take this game to its full potential and will be able to explain how to win with any target number and any range of consecutive numbers (starting with $1$).

Before moving on to a few other kinds of games, I'd like to mention another numerical strategy game which has mathematical links to Got It!. It is called The Factors and Multiples Game:

This is a game for two players.
You will need a $10$ by $10$ number grid (with the numbers from $1$ to $100$):

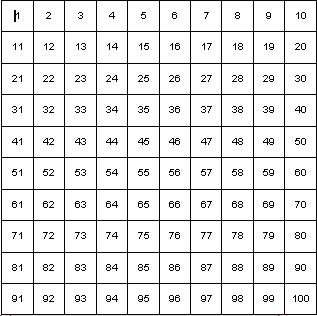
The first player chooses a positive even number that is less than $50$, and crosses it out on the grid.
The second player chooses a number to cross out. The number must be a factor or multiple of the first number.
Players continue to take it in turns to cross out numbers, at each stage choosing a number that is a factor or multiple of the number just crossed out by the other player.
The first person who is unable to cross out a number loses.

You could introduce this on an OHP or just have the image on an interactive whiteboard and use the pen tool to cross out numbers. As ever, the important question is how you can guarantee a win. I urge you to try this out - it leads to a very satisfying strategy based on factors, multiples and prime numbers!

There are many suggestions on NRICH for games that use playing cards and Stop or Dare is one that is easy to get the hang of:

For this game you just need a pack of cards. You can play by yourself, but it 's more fun with two or three players.
Shuffle the pack and place it face down.

Set a target score for the game, for example 100. The first player turns over the top card and continues turning over cards, adding together the value of each card, until he/she decides to stop. (Jacks = 11, Queens = 12.) When the player stops, the total is recorded as his/her score. However, if an Ace or King is turned over, no points are scored at all and the turn is finished.
Now the second player starts turning over cards in the same way. Players continue having turns and building their scores until someone reaches the target score. This player is the winner. If the cards are all turned over before the target is reached, just reshuffle the pack and continue.

Is there a strategy that increases your chances of winning?
How many cards should you risk turning over before you stop?
Does it pay to be daring?
Does it matter how many people play or who goes first?
What difference does the target score make to the game?

An alternative version of the game is to play so that if you pick up a Queen or a King, no points are scored and your turn ends; and if you pick an Ace, all your points are lost and you must start again from zero. Whichever rules you use, this card/arithmetical/strategy game will provoke lots of discussion. Using the final questions listed above in the problem text, you can challenge children to think more deeply about how they play the game and to begin to make conjectures, then back up their conjectures with explanations. The game provides a different context for talking about probability (although you may have to spend some time investigating a pack of playing cards beforehand, depending on the experiences of your class).

Having given you some examples of games on NRICH, let me return to the questions I asked at the beginning of this article: Is it enough that children might "have fun" playing mathematical games? Can we justify their use in the classroom? I guess my answers would be no and yes respectively, and of course the two are linked. Looking at the games I've described here, all of them require application of mathematical knowledge and/or skills, and perhaps more importantly, the knowledge and skills are needed not just to understand how to play the game and therefore potentially "have fun", they are needed to develop a strategy in order to guarantee a win. This strategy development requires higher-order thinking and I think this is what justifies their use in the classroom.

Of course, there are many other reasons to use mathematical games, and the motivating factor is certainly one, but I don't think it is sufficient on its own. Games can give meaningful situations for children to apply their mathematics and can provide a non-threatening environment, which may help to boost children's confidence and change their attitudes towards the subject. Many of the games I have mentioned are accessible and can be taken to different levels without having to differentiate (low threshold high ceiling) and therefore can provide a great assessment opportunity for you. In another article, Using Games in the Classroom, Gillian Hatch argues that the reasons for including games in mathematics can be separated into three types: learning, ways of working and pupil experience. Her article is well-worth a read, and although it is written with secondary teachers in mind, it is very applicable to primary classrooms too.

I do hope you will seek out some of the games and related articles on NRICH, and feel confident that their use in your classroom can be completely and utterly justified.

This article first appeared in Primary Mathematics, a journal published by The Mathematical Association.