At Luke's request, we began with one of the BEAM cards. He had tried a few of these already with his Dad and seemed keen to have a go at some more (perhaps to get further through the box than his older sister!). We started with the Counter-Counting Puzzle, which begins like this:

Even before we had begun the problem itself, Luke demonstrated his awareness of, and familiarity with, number by counting out the twelve counters that we needed in twos. At first, we spent a minute or so just checking we understood what the instructions were asking of us, for example, "How many counters could we move into this pile?". It was interesting for me that Luke launched himself eagerly into the task. He did not appear to worry initially about getting the "right" answer, he was simply keen to have the same number of counters in each pile. As he moved counters from one pile to another, I tried not to interfere with his choices, except to remind him of the rule. He was triumphant on reaching a solution. When I enquired how many moves it had taken, he had no idea. I think this first go for him had been about understanding and internalising the task rather than worrying about how long it took. Now with this extra challenge, Luke asked me to count the number of moves as he manipulated the counters. He appeared a little concerned that he wouldn't be able to remember how he had done it, but that didn't hold him back for long.

So, with Luke moving counters and me counting aloud, he managed to finish with three piles of four counters in three moves:

6, 5, 1
6, 4, 2
6, 2, 4
4, 4, 4

I asked, "Do you think you can do it in fewer moves?". Luke's response was to try, but again he managed three. "Look in the book, look in the book!" he suggested. Luke wanted confirmation from the teacher's book that he had succeeded. This was an interesting dilemma for me. Which should come first - analysing what we could do at each stage to convince ourselves what the fewest number of moves was, or having been told it could indeed be done in a particular number of moves, trying to find out how? I sensed that Luke would have been happier with the latter (was that a "cop-out" on my part?!), so we looked in the book. Of course, we read that in fact it could be done in only two moves. "That's impossible!" cried Luke, but in an I-still-want-to-work-out-how way rather than an I'm-giving-up way. It was then that I felt my role of prompter was really needed. We took it step by step, looking at the different possibilities: "What could we do now?" and in this way, Luke quickly arrived at a solution in two moves.

I feel it is worth pointing out that at this stage we hadn't written anything down, and in fact we didn't at any point as we worked on this problem. Retrospectively, perhaps I should have encouraged Luke to address the issue of recording, but it didn't seem to be hindering him enough to warrant attention at the time. If we had recorded what Luke had tried, it might have helped him see the two moves more quickly. It would also have facilitated other questions, such as "Can we do two moves in another way?"; "Will we always end up with four in each pile?"; "How do you know?" ... Should I have suggested to Luke that he could write things down? I wonder if he wanted to, but didn't ask?

Having gone through the process of analysis together, Luke seemed to gain in confidence. The BEAM activity goes on to suggest starting with the counters in different piles. Luke's own example was $1$, $1$, $10$ and he was able to cope well with my questioning: "How do you know you can't do it in fewer moves?". His justifications centred on looking at the different possibilities at each stage, as we had done together. He was able to articulate that he couldn't move any counters into the pile of $10$, so he would move one from the $10$ into one of the piles of $1$. Again, he couldn't move any into the resulting pile of $9$, so would move two out and so on.

Working with Luke in this way highlighted for me the power of this task in encouraging young children to begin to work in a systematic way, justifying choices and decisions as they go. Who says that primary-aged children can't prove results mathematically?

The second activity that I had chosen, called Secret Number, was taken from NRICH and was published in July 2007.

So, Luke and I played a version of this game. I told Luke that I was putting a secret number into my calculator and then I was adding five. I pressed the equals button and showed Luke that the answer was $8$. Could he work out what my secret number was?

Without hesitation, Luke picked up his own calculator and, after thinking for a few seconds, began to press keys. He didn't say out loud what he was doing but after pressing equals, he expressed delight. He too had $8$ on his display. "What was my secret number, then?" I asked. The reply was a confident one: "$3$". "How did you work it out?" I enquired. Luke described how he counted on from $5$ to $8$ in his head, which needed $3$. Using the calculator, he had performed the same calculation as I had, as a check. I was delighted. Such a simple question had revealed to me exactly what Luke understood by addition. It was obvious to him that addition is commutative - that if $3 + 5 = 8$, then $5 + 3$ is also $8$.

I wondered whether counting on was Luke's only strategy, or whether he had others to draw on. So, I told him that my new secret number added to $10$ was $20$, and showed him the calculator display. This time, Luke knew that $10$ add $10$ is $20$ without any mental calculation, it was a fact that he was familiar with, but he did check the sum on his calculator once again.

I invited Luke to think of a secret number and to see whether I could work out what it was. This seemed to appeal to him, so after a short time he told me that he'd put his number into the calculator, then pressed add $100$ (checking with me that he had entered $100$ correctly), then equals. He showed me the result of this addition, which was $101$. I knew Luke was very familiar with numbers up to $100$ - he'd told me that on the way to see me, he and his Dad had counted all the way from $1$ to $100$ and then in twos up to $100$ - but he wasn't sure how to read the number on the display. I read out "one hundred and one", explaining a little by breaking it up into the $100$ and the $1$, pointing to the display at the same time. I imagine that adding a large number had appealed to him, thinking it would be much harder for me to work out his secret number. It was fascinating to see that as soon as the total was said aloud, he immediately realised what an "easy" task he had set me.

Building on this, I did the same, adding $100$ to a new secret number, resulting in $116$ which we read together from my calculator. Unsurprisingly, Luke needed no prompting and was able to verify my number immediately. I decided to take this idea in a slightly different direction, hoping to gain more insight into Luke's understanding of place value. This time, I added $50$ to a different secret number and got $56$. This did not phase Luke at all, as I'd anticipated. So, I thought I would push him a little. Sticking with adding $50$, I now got a total of $71$ on my display. This took several stages. Having started with $9$, and so obtaining $59$, we talked about whether we needed a bigger or smaller number than $9$ if we were aiming for $71$. So, Luke tried $10$ to get $60$. This produced an "Aah!" and Luke began with $20$ to get $70$. He then knew immediately that he needed one more, so told me that it would be $21$ before he used the calculator as the checking mechanism.

Would Luke be able to use that calculation in the next? I added $50$ to another secret number and the total was $81$. Whether Luke didn't remember what the previous addition had been, or whether it just didn't occur to him that it might have been useful, I'm not sure. What he had appeared to take on board was that my number was going to be larger than $10$. He tried $48$ but realised the total was too big. So, he then tried $38$, which of course made $88$. This was the breakthrough moment - he was certain then that my number was $31$.

Afterwards, I was struck by the fact that playing this game with Luke, which was based on such a simple idea, had revealed huge amounts about his understanding of place value and addition. It was a humbling process for me as the "teacher" in the sense that without the conversations we had, I would have jumped to inaccurate conclusions about the level of Luke's understanding. Talking as we went along meant that Luke's thought processes were gradually revealed to me and the more I discovered, the better I felt I was able to encourage him and push him further.

In the last ten or fifteen minutes of our time together, we looked at a third problem based on Caterpillars, published on NRICH in September 2007:

Our caterpillars have numbers on each little part - numbers $1$, $2$, $3$, $4$, ... up to $16$.

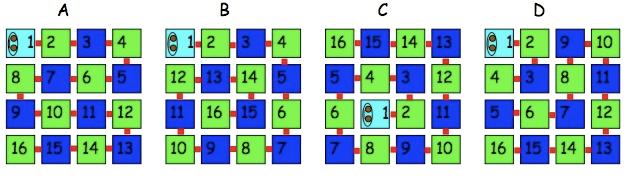
You can see their pale blue head, and their body bending at right angles so that they are lying in a square.

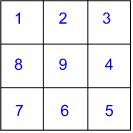
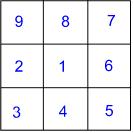
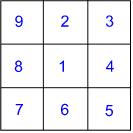
"Can we do diagonals?" he enquired. I thought that we probably could and in this way he actually made the problem more challenging. As he began to layout the counters, incorporating a diagonal arrangement, he realised that he was more restricted. He talked as he went along, looking ahead to see whether, if he put that counter there, he was going to be able to place the rest of the caterpillar. He was able to answer my questions as to why he'd had to change the position of one segment, for example, in order to be able to complete the arrangement.

As he had made the different arrangements, he had recorded the numbers in his own hand-drawn grids. He suddenly decided that he would join the numbers in numerical order with straight lines. I'm not sure what prompted him to do this - it wasn't my instigation - but what was wonderful was that he immediately remarked that the first two arrangements created the same pattern of lines. He clearly had not predicted this and found it fascinating. This felt as if it was his own investigation. He was definitely leading the way quite happily and in this instance, it led to an interesting question: why are they the same? I wonder whether this has ever happened to you as you've worked on some mathematics? Two results are the same and what a fantastic feeling it is to be able to explain why, even though you had not anticipated it happening. How powerful mathematics feels during those moments!

As I intimated at the beginning of this article, I was in a luxurious situation. How often do we as teachers have the opportunity to work on a one-to-one basis with any of our pupils? And yet how valuable those opportunities can be. While working with Luke, I was particularly struck by the fact that he was prepared to have a go at each task. Was this the attitude he always adopted? Was it the fact that there weren't any peers to judge him? Was it that he regarded our time together as "fun" and was therefore more relaxed? I don't know. But it made me reflect on where children pick up a reluctance to "play with the mathematics" from? Is this something we value and therefore should be actively encouraging more often? The conversations Luke and I had as we worked together enabled me to probe quite deeply what Luke was happy with. I was able to judge his zone of proximal development and move him on appropriately. Subtleties and nuances in his understanding were revealed which would almost certainly have passed me by had I been in a room with twenty nine other children. However, to some extent, I still felt that I was making decisions on the spur of the moment which may not have been the best in hindsight, just as we do in the classroom.

So, I'm not sure what I conclude. I guess I'm saying that we should try and grab every opportunity to engage in mathematical conversations with our pupils, although it's never going to be easy. We're never going to be able to support every child in a class as we might if we were working with each one individually. But perhaps we could just take stock and ask ourselves: are we sure they have grasped that idea? What questions could we ask to probe a little more deeply?

Thank you for indulging me.

Thank you also to Luke and his Dad.

This article first appeared in Primary Mathematics, a journal published by The Mathematical Association.