 Links to the NRICH website Home page
Links to the NRICH website Home page

30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Christmas Chocolates



Penny, Tom and Matthew were each given mint chocolates in a hexagonal box:
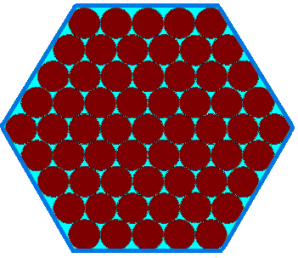



Penny, Tom and Matthew have been promised a larger box of chocolates as a Christmas present from their grandmother. The box will have $10$ chocolates along each edge, instead of just $5$.
How
would each child work out how many chocolates the larger box will
contain?
Can you describe any other ways to
work it out?
Here are some more questions you might like to consider:
- For which sizes of chocolate box will the three children be able to share the chocolates equally?
- For which sizes of chocolate box will the boys be able to share the chocolates equally?
- Can you describe how each child would work out the number of chocolates in a box with $n$ chocolates along each edge?
You may also like
Summing Consecutive Numbers
15 = 7 + 8 and 10 = 1 + 2 + 3 + 4. Can you say which numbers can be expressed as the sum of two or more consecutive integers?
Always the Same
Arrange the numbers 1 to 16 into a 4 by 4 array. Choose a number. Cross out the numbers on the same row and column. Repeat this process. Add up you four numbers. Why do they always add up to 34?
Fibs
The well known Fibonacci sequence is 1 ,1, 2, 3, 5, 8, 13, 21.... How many Fibonacci sequences can you find containing the number 196 as one of the terms?