Copyright © University of Cambridge. All rights reserved.
'Cyclic Quadrilaterals' printed from https://nrich.maths.org/
Show menu
Cyclic Quadrilaterals printable sheet
Printable sheets of circles: 9 dot 10 dot 12 dot 15 dot 18
dot
In the GeoGebra interactivity below there is a circle with 9 equally spaced points on the edge, and one in the centre.
Draw as many different triangles as you can, by joining the centre dot and any two of the dots on the edge.
Can you work out the angles in your triangles?
You should have found four different triangles with angles of:
80, 50, 50
120, 30, 30,
160, 10, 10
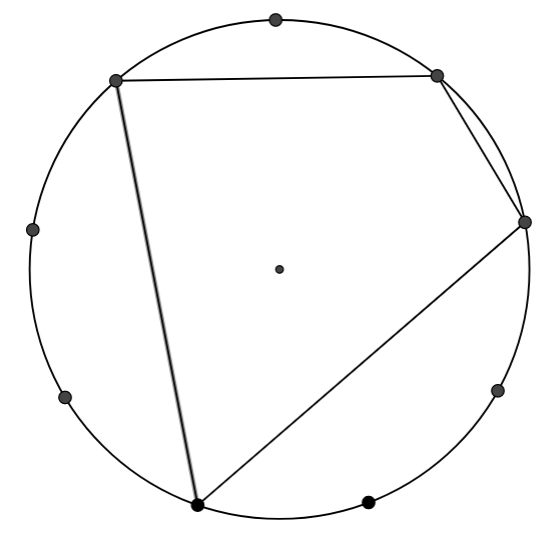 Now draw a few quadrilaterals whose interior contains the centre of the circle, by joining four dots on the edge.
Now draw a few quadrilaterals whose interior contains the centre of the circle, by joining four dots on the edge.
Can you work out the angles of your quadrilaterals?
If you're finding it hard to work out the angles, take a look at Getting Started.
Create at least five different quadrilaterals in this way and work out their angles.
What do you notice about the angles on opposite vertices of your quadrilaterals?
Perhaps you are wondering whether this only happens with 9-dot circles...
You may wish to explore the opposite angles of quadrilaterals on circles with a different number of dots.
Click below for interactivities with 10, 12, 15 and 18 dots around the circle.
10 dots
12 dots
15 dots
18 dots
Extension:
Will the same happen if you draw a circle and choose four points at random to form a quadrilateral?
To prove that the opposite angles of all cyclic quadrilaterals add to $180^\circ$ go to Cyclic Quadrilaterals Proof
Quadrilaterals whose vertices lie on the edge of a circle are called Cyclic Quadrilaterals.