Copyright © University of Cambridge. All rights reserved.
'How Steep Is the Slope?' printed from https://nrich.maths.org/
Show menu
Jordan from Paul H. Cale Elementary listed 24 gradients that could be made on the grid after coming up with a systematic method to find them and correctly identified that the gradient of a vertical line is undefined (as it requires division by zero).
Once I understood the problem I printed out the work page and started just drawing random lines, this did not work so I looked at your hint and tried it the way it said to (make all the lines you can that connect to another point from U) and, it worked!! Once I got the hang of it, it went really fast!! I didn't even have to figure out the negative ones because I knew that they would be the same as the positive ones, just negative.
All the possible positive ones are:
| $4$ | $\frac{1}{3}$ |
| $3$ | $\frac{1}{4}$ |
| $2$ | $0$ |
| $1 \frac{1}{2}$ | |
| $1 \frac{1}{3}$ | |
| $1$ | |
| $\frac{3}{4}$ | |
| $\frac{2}{3}$ | |
| $\frac{1}{2}$ |
and the negative ones....
| $-4$ | $-\frac{1}{3}$ |
| $-3$ | $-\frac{1}{4}$ |
| $-2$ | $-0$ |
| $-1 \frac{1}{2}$ | |
| $-1 \frac{1}{3}$ | |
| $-1$ | |
| $-\frac{3}{4}$ | |
| $-\frac{2}{3}$ | |
| $-\frac{1}{2}$ |
The Gradient for a straight vertical line is undefinable.
Jordan lists both 0 and 0- as gradients - is there a difference?
Samantha from Aylesbury High School gave a very clear explanation of how all the different possible gradients could be identified
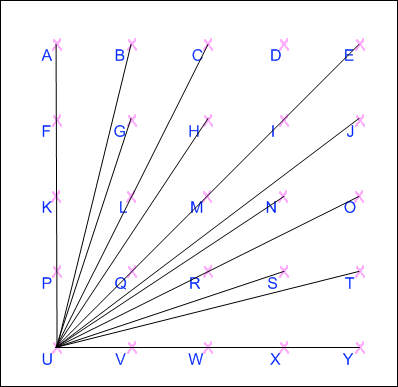
In a), I know I have found all of the positive gradients because, starting at point U, I have drawn lines to every other point. Some lines have the same gradient, but because they start from the same point they become the same line, but passing through several points. If I were to start from any point on the grid other than Y and draw a line from it to another point that line would have the same gradient as one which started from Y (or Y on the grid b).
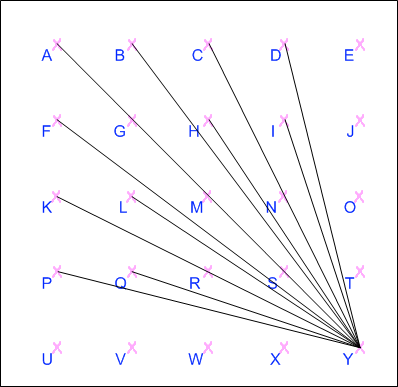
In b), I know I have found all of the negative gradients because, starting at point Y, I have drawn lines to every other point. Some lines have the same gradient, but because they start from the same point they become the same line, but passing through several points. If I were to start from any point on the grid other than Y and draw a line from it to another point that line would have the same gradient as one which started from Y (or U on the grid a). I have excluded the lines with a gradient of 0 and 8 because they are both on a).
These are all 24 of the gradients shown on the two diagrams, and the points they pass through:
In a), I know I have found all of the positive gradients because, starting at point U, I have drawn lines to every other point. Some lines have the same gradient, but because they start from the same point they become the same line, but passing through several points. If I were to start from any point on the grid other than Y and draw a line from it to another point that line would have the same gradient as one which started from Y (or Y on the grid b).
In b), I know I have found all of the negative gradients because, starting at point Y, I have drawn lines to every other point. Some lines have the same gradient, but because they start from the same point they become the same line, but passing through several points. If I were to start from any point on the grid other than Y and draw a line from it to another point that line would have the same gradient as one which started from Y (or U on the grid a). I have excluded the lines with a gradient of 0 and 8 because they are both on a).
These are all 24 of the gradients shown on the two diagrams, and the points they pass through:
| Gradient | Points it passes through |
|---|---|
| $\infty$ | AFKPU |
| $4$ | BU |
| $3$ | GU |
| $2$ | CLU |
| $1.5$ | HU |
| $1 \frac{1}{3}$ | DU |
| $1$ | EIMQU |
| $0.75$ | JU |
| $\frac{2}{3}$ | NU |
| $0.5$ | ORU |
| $\frac{1}{3}$ | SU |
| $0.25$ | TU |
| $0$ | UVWXY |
| $-0.25$ | PY |
| $-\frac{1}{3}$ | QY |
| $-0.5$ | KRY |
| $-\frac{2}{3}$ | LY |
| $-0.75$ | FY |
| $-1$ | AGMSY |
| $-1 \frac{1}{3}$ | BY |
| $-1.5$ | HY |
| $-2$ | CNY |
| $-3$ | IY |
| $-4$ | DY |
Ryli from Aylesbury High School came up with a excellent method for deducing how many different gradients could be constructed on a 4 by 4 grid, looking at all possible combinations of steps and then discounting those which were repeated.
There are 24 different gradients.
You can go between 1 and 4 units (inclusive) horizontally (e.g. A-E) and between 1 and 4 units (inclusive) vertically (e.g. A-U) in any combination:
$$ \begin{array} & \frac{1}{1} & \frac{2}{1} & \frac{3}{1} & \frac{4}{1} \\ \frac{1}{2} & \frac{2}{2} & \frac{3}{2} & \frac{4}{2} \\ \frac{1}{3} & \frac{2}{3} & \frac{3}{3} & \frac{4}{3} \\ \frac{1}{4} & \frac{2}{4} & \frac{3}{4} & \frac{4}{4} \\ \end{array} $$There are sixteen combinations (4x4), but gradients are found by the horizontal being divided by the vertical so some of them cancel down to be the same as others (e.g. 1/2=2/4). Taking out the repeated ones gives:
$$ \begin{array} & \frac{1}{1} & \frac{2}{1} & \frac{3}{1} & \frac{4}{1} \\ \frac{1}{2} & & \frac{3}{2} & \\ \frac{1}{3} & \frac{2}{3} & & \frac{4}{3} \\ \frac{1}{4} & & \frac{3}{4} & \\ \end{array} $$There are 11 combinations left, but each one can be positive or negative, so there are actually 22 gradients.
We now have 2 more things to consider. Although 0 cannot be divided by anything, you can divide anything by 0 to give 0 as a gradient on a straight vertical line. This adds 1 more posible gradient. Likewise you can have infinity ($\infty$) as your gradient on a straight line horizontally, so this is the 24th gradient.