Copyright © University of Cambridge. All rights reserved.
'Summing Squares' printed from https://nrich.maths.org/
Show menu
You may wish to make six copies of each square prism below to aid you in visualising the problem that follows.
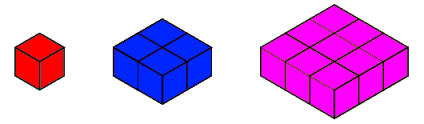
If I take six of the
red cubes I can make this 3 by 2 by 1 cuboid:

I want to surround this with blue
cubes to make the 5 by 3 by 2 cuboid below:
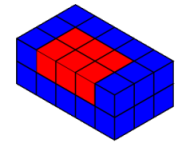
Could I build this cuboid by adding on six blue square prisms like the
one above without splitting any of them?
If so, describe how to do it. If not, explain why not, and
describe how to arrange the blue square prisms so that as few as
possible need to be split.
I want to surround this with pink
cubes to make a 7 by 4 by 3 cuboid. (See Hint for a picture of this
cuboid.)Could I build it by adding on six pink square prisms like the
one above? Do I need to split any this time?
So far, we've discovered that
$$6 \times 1^2 = 3 \times2 \times1$$
$$6\times(1^2+2^2) = 5\times3\times2$$
$$6\times(1^2+2^2+3^2) = 7\times4\times3$$
Can you describe a method for forming the next cuboid in the
sequence by adding on six
square prisms? You will only need to split one of your square
prisms each time. Does the sequence continue forever?
Work out the dimensions of the $n^{th}$ cuboid.
Can you explain how to make the $(n+1)^{th}$ cuboid from it?
What are the dimensions of the $(n+1)^{th}$ cuboid?
How could these ideas be used to calculate the sum $1^2+2^2+3^2+...+n^2$ quickly for any value of $n$?