 Links to the NRICH website Home page
Links to the NRICH website Home page

30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Weighty Problem



- Problem
- Student Solutions
We have two splendid solutions here. The first is from Vassil from Lawnswood High School, Leeds, and it is in a series of diagrams that speaks for itself.
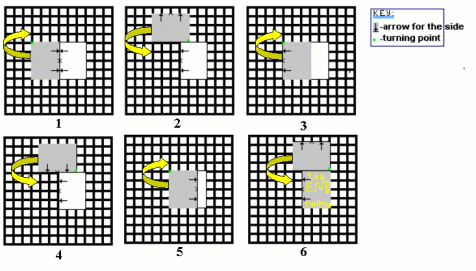
Here is a different solution from Edwin, The Leventhorpe School, Sawbridgeworth.
I'm on a roll (I hope). Here is my solution to the Tough Nut "Weighty Problem". Your Hint suggests that only 5 moves are needed, but I have used 6. I think I have made things too difficult for myself by being too cunning. As my solution is essentially a series of diagrams I have decided to include an account of how I found my solution.
To work this puzzle out I had to use quite a bit of intuition. The most shaky piece of intuition was coming up with moves 1 and 2, which I choose because they flipped the cabinet, but did not put it in an obvious place. I probably wanted it like this because I assumed the solution would involve the cabinet being in complex positions. I then ran out of inspiration for a third move and decided to look for more clues. Recognising that the rectangle could be thought of as two 3 by 4 triangles, I remembered the Pythagorean triple 3 4 5 and realised that the diagonals of the cabinet were exactly 5 squares long. I played around with moving the shape using its diagonals and came up with moves 5 and 6, but didn't have anywhere to use them. All that was left was a bit of old fashioned guess work to try and connect the moves I had thought of, and I eventually stumbled across moves 3 and 4, and thus the whole solution.
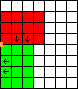
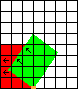
In the following diagrams, the area in red represents the position of the cabinet at the start of the move, and the area in green represents the position of the cabinet at the end of the move. The small orange square represents the corner about which the cabinet is rotated. The arrows show which way the cabinet is facing. All the pictures are based on the same 7 by 8 grid so you can see all the moves relative to the initial position of the cabinet.
| Move 1: | Move 2: | Move 3: |
|---|---|---|
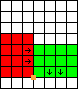 |
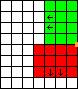 |
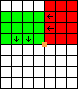 |
| Move 4: | Move 5: | Move 6: |
 |
 |
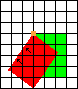 |
(The picture above does not show the arrows on the green area, but they would be facing left, so that the green area was a mirror image of the red area in the first picture).
The cupboard can be turned around in 5 moves and we leave that as a further challenge. Try turning it through 180 ° in two moves then, taking symmetry into account, it can be shunted into the final position in three moves.
You may also like
All in the Mind
Imagine you are suspending a cube from one vertex and allowing it to hang freely. What shape does the surface of the water make around the cube?
Instant Insanity
Given the nets of 4 cubes with the faces coloured in 4 colours, build a tower so that on each vertical wall no colour is repeated, that is all 4 colours appear.