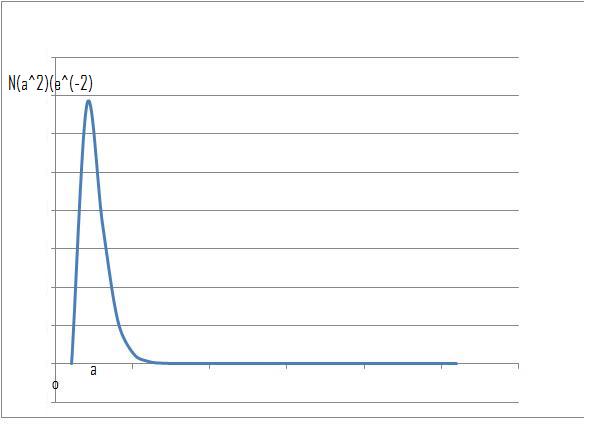
1. A radial probability density function for an electron orbit

$$f(r) = Nr^2e^{-\frac{2r}{a}}$$

I feel that the easiest way to think of this curve is to first consider the curves $r^2$ and $e^-r$ separately, then consider the shape of the curve produced when multiplying the two together.

$r^2$ grows with r whilst $e^{-r}$decays to 0 with increasing r

when $r$ is very small $e^{-r}$ $\approx$ 1, therefore the curve is effectively $r^2$.
when $r \to \infty$ then $e^{-r} \to 0$, when we multiply the two numbers together a very small number will therefore result.

At $r = 0$, $f(r) = f(0) = 0$

at $f(r) = 0$
either $r^2= 0$ therefore $r = 0$
or $e^{\frac{-2r}{a}} = 0 $ therefore $r =\ln(0) = \infty$
as $r \to \infty$ we have $f(r) \to 0$

If we now differentiate the function we will be able to find its turning points

$$ \frac{d}{dr} Nr^2e^{-\frac{2r}{a}}= 2Nr(1 - \frac{r}{a})e^{\frac{-2r}{a}}$$

When $ \frac{d}{dr} = 0$ we find $r =0$, $r= a$ and $r = \infty$.

If we now differentiate once more to determine the nature of each of the turning points we find that:

$$ \frac{d^2f}{dr^2}= \frac{d}{dr}2Nr(1 - \frac{r}{a})e^{\frac{-2r}{a}}
=2(1-\frac{r}{a} + )(2r)(\frac{-1}{a}))Ne^{\frac{-2r}{a}} + (\frac{-2}{a}(2r)(1 - \frac{r}{a})Ne^{\frac{-2r}{a}}$$

at $r = 0$: $ \frac{d^2f}{dr^2}=2N$ which is greater than $0$, therefore $r = 0$ is a minimum

at $r = \infty$: $ \frac{d^2f}{dr^2}= 0$

at $r = a$: $ \frac{d^2f}{dr^2}=-2Ne^{-2}$ which is less than $0$, therefore $r = a$ is a maximum.

From the above information we can deduce the general shape of $f(r)$ as shown below.
(Note: The graph below has been plotted assuming all constants equal 1 )

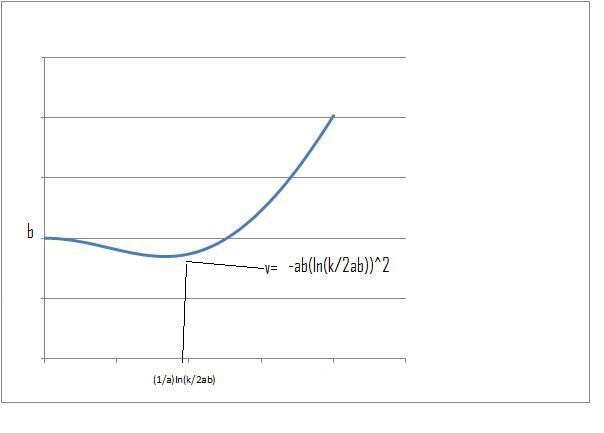
2. Potential energy for the vibrational modes of ammonium

$$ V(x)=\frac{1}{2}kx^2+be^{-ax^2} $$

When $x$ is very small $v(x) \approx be^{-ax^2}$
and when $x$ is large $e^{-ac^2} \to 0$, $v(x) \approx \frac{1}{2}kx^2$

when $x = 0$, $v(0) = b$ by inspection it can be deduced that $v(x)$ can never reach $0$ as $be^{-ax^2}$ is always greater than $0$ and $\frac{1}{2}kx^2$ is greater than $0$ at all $x$ except $x=0$, but at this point $be^{-ax^2}= b$

as $x \to \infty$ we have $v(x) \to \frac{1}{2}kx^2 \to \infty$

If we now differentiate the function we will be able to determine its turning points.

$$ \frac{dv}{dx} = xk - 2abxe^{-ax^2} = x\left(k-2abe^{-ax^2}\right)$$

when $ \frac{dv}{dx} = 0$ we find $x = 0$ and $(k-2abe^{-ax^2}) =0$
therefore $x = \sqrt{\frac{-1}{a}\ln\left(\frac{k}{2ab}\right)}$

If we now differentiate once more to determine the nature of each of the turning points we find that:

$$ \frac{d^2v}{dx^2}= k - 2abe^{-ax^2} + 4a^2bx^2e^{-ax^2}$$

at $x = 0$, $ \frac{d^2v}{dx^2}= k- 2ab$ , the nature of this turning point will therefore depend on the relative magnitudes of the constants $a$, $b$ and $k$. If $k$ is greater than $2ab$, $x=0$ will be a minimum but if $2ab$ is greater than $k$ it will be a maximum.

at $x= \sqrt{\frac{-1}{a}\ln\left(\frac{k}{2ab}\right)}$ we should expect a minimum (or possibly a point of inflexion) as a consequence of the fact that as there are only two turning points and as $x \to \infty$ $v(x) \to \infty$ (it therefore cannot be a maximum).