Links to the University of Cambridge website
 Links to the NRICH website Home page
Links to the NRICH website Home page

 Links to the NRICH website Home page
Links to the NRICH website Home page

Nurturing young mathematicians: teacher webinars
30 April (Primary), 1 May (Secondary)
30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Eudiometry
Age 16 to 18
Challenge Level 





- Problem
- Getting Started
- Student Solutions
In this problem, consideration of the ideal gas equation is important. At a basic level we know that a mole of substance in gaseous form occupies a volume of roughly 24dm$^3$. The ideal gas equation, $pV = nRT$ has several variables, but at constant temperature and pressure it can be seen that $V = n(\frac{RT}{p})$ where the bracketed term is a constant (R being the ideal gas constant). Thus volume varies directly with number of moles for an ideal gas so consideration of molar changes is sufficient throughout this question.
On combustion of ethane, the balanced equation shows that 2 + 7 = 9 molar units of reactants interact to produce 4 + 6 = 10 molar units of products. As the volume occupied by a mole of gas is considered to be the same regardless of the species involved and that all species are in gaseous form, the volume of the gas must increase proportionally to the increase in moles that has occured.
If you now consider the case for a generic hydrocarbon, we can first analyse the volumetric change for alkanes, which have a generic formula C$_n$H$_{2n + 2}$, and alkenes or cyclic alkanes which have a general formula C$_n$H$_{2n}$. These examples cover the most widely encountered hydrocarbons. A further calculation may be conducted for benzene.
Alkanes
C$_n$H$_{2n + 2}$ + $\frac{3n + 1}{2}$O$_2$ $\rightarrow$ nCO$_2$ + (n + 1)H$_2$O
so in terms of a molar change:
$1 + \frac{3n + 1}{2}\rightarrow 2n + 1$
Proportional increase in moles
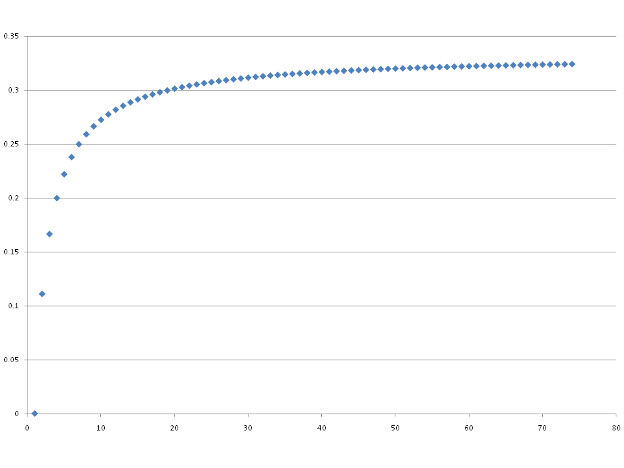
Number of carbon atoms
It can be seen that the increase in
gaseous volume on combustion is by no means assured for all
hydrocarbons. For CH$_4$ for example, there is no increase in the
number of moles of gas on combustion. As alkanes get larger the
proportional increase in volume increases and tends to 0.33 due to
the dominance of $\frac{3n}{2}$ for the left hand side and 2n for
the right hand side of the equation at large values of n in
determining the number of moles.
$\frac{2n -
\frac{3n}{2}}{\frac{3n}{2}}$ = 0.33 (2dp).
Thus large chain alkanes produce a
large change in volume as although the percentage change tends to
33%, the actual number of reactant moles increases considerably
with the addition of 1.5 molar units for total reactant moles for
an increase of a single carbon.
Alkenes
Alkenes show a very similar
relationship to that above.
C$_n$H$_{2n}$ + $\frac{3n}{2}$O$_2$
$\rightarrow$ nCO$_2$ + nH$_2$O
In terms of the molar changes:
1 + $\frac{3n}{2}$ $\rightarrow$
2n
Again, the percentage increase in
volume tends to 33% as with alkanes. Yet for each species
equivalent in terms of the number of carbons to a certain alkane,
the actual increase in moles is slightly greater for the alkane due
to the presence of a greater number of hydrogen atoms in the
species (and the fact that a single molecule of oxygen is utilised
to generate two water molecules). Note also that ethene is the
alkene species for which there is no increase in volume on
combustion.
Cycloalkanes have the same general
formula as alkenes but obviously it is impossible to produce a two
membered ring structure.
As a point of interest, benzene has
a molecular formula C$_6$H$_6$ and its complete combustion in
oxygen is given below.
C$_6$H$_6$ + $\frac{15}{2}$O$_2$
$\rightarrow$ 6CO$_2$ + 3H$_2$O
8.5 moles $\rightarrow$ 9
moles
This corresponds to a marginal
increase in volume. Considering the trends for these types of
molecules it is clear that the molar increase in volume is greatest
for long chain alkanes due to the fact that these a saturated
molecules which require a large number of reactant oxygen molecules
for combustion.
As we have seen, if the total volume
of gas is unchanged by reaction the number of moles on the left and
right hand sides should be equivalent. An example of a reaction
where the number of moles of gas remains unchanged is:
N$_2$ + O$_2$ $\rightarrow$
2NO
Can you think of
any other examples?