 Links to the NRICH website Home page
Links to the NRICH website Home page

30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Sticky Numbers



- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
Well done to James and Joshua from RMH Hospital Schoolroom in the UK, Jose, Veer and Edward from Dulwich College in the UK, Raul and Belen from Cambridge House Community College Valencia in Spain, Laila from England, Amy from Hutchesons’ Grammar in Scotland, Dang Le Anh from Delta Global School in Vietnam, Muhammad Mustafa from Pakistan, Anson, Zahra and Julia from St Mary's College in the UK, Chris from the USA, Rohan from Wilson's School in the UK and Ci Hui Minh Ngoc Ong from Kelvin Grove State College (Brisbane) in Australia who each submitted a solution getting the 17 numbers in the right order, that is:
\[16\quad 9\quad 7\quad 2\quad 14\quad 11\quad 5\quad 4\quad 12\quad 13\quad 3\quad 6\quad 10\quad 15\quad 1\quad 8\quad 17\]
We also received some fantastic explanation. Rohan and Anson started by thinking about the square numbers available. Anson wrote:
Find the ways adding up to every square number until 25 and just put them together without repeating any number.
Other people started by thinking about the numbers available. James and Joshua started with the largest numbers:
[We] worked out that 16 could only be joined to 9 and so had to be at one end. This first attempt came to a dead-end [so we] began to systematically look at other large numbers and how they would need to be paired. [We] found that they all needed to be paired with two particular lower numbers, and used this information to create a chain that worked.
Jack from Concordia Lutheran School in the USA, Chris and Edward also started from the ends. This is Jack's work:

Veer noticed some patterns:
17, 8, 1, 15, 10, 6, 3, 13, 12, 4, 5, 11, 14, 2, 7, 9, 16.
O, E, O, O, E, E, O, O, E, E, O, O, E, E, O, O, E
Key: O-odd E-even
As you can see they all add up to a square number.
The pattern is that they add up like this: 25, 16, 9, 16, 25 and it repeats.
Laila believed there was only one possible chain (which could go in either direction). Can you see how James and Joshua's method adds more evidence to Laila's argument?
This is a unique solution because for the lowest number, 1, there are only two choices, 1 + 8 = 9 or 1 + 15 = 16. We can see that the only option for 17 would be 8 because 17 + 8 = 25. This shows that there is only one order to begin - 17, 8, 1, 15 and this will carry on since each number will only have two other numbers less than 17 that can be added to make a square. One other number, 16,
only has 9 that can be added to make a square, so this
must be at the end of the sequence.
Amy built on this idea to show that the solution really is unique (click on the image to enlarge). Are there any possible connections that Amy missed?
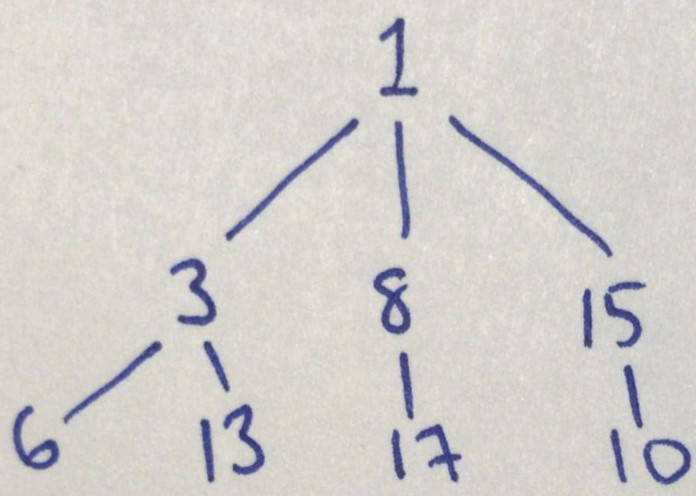
Muhammad Mustafa showed the pairs of numbers on a tree diagram:
I made a tree diagram starting with one and extending it to the number(s) that it can be arranged with. I then did the same with the new number(s) and kept on going until there were no more numbers to choose from. The tree diagram looked a bit like this (this is just a portion of it):
Instead of seeing which other numbers each number should be paired with, Dang Le Anh focused on which square numbers each number could make. This led to the same solution, and a different way of showing that the solution is the only possible solution (click on the image to download the full-size version):
Ci Hui Minh Ngoc Ong used similar ideas to show that there is only one solution, and also found some patterns. Click here to see Ci Hui Minh Ngoc Ong's work on paper, and here to download the spreadsheet that Ci Hui Minh Ngoc Ong created.
You may also like
Time of Birth
A woman was born in a year that was a square number, lived a square number of years and died in a year that was also a square number. When was she born?
Square Routes
How many four digit square numbers are composed of even numerals? What four digit square numbers can be reversed and become the square of another number?

