Copyright © University of Cambridge. All rights reserved.
'The Development of Algebra - 2' printed from https://nrich.maths.org/
Show menu
The first part of this brief history of algebra focussed on the important practical origins of the problems that led to the procedures we have for solving equations, and the ways in which the problems were visualised as manipulation of geometrical shapes.
This second part shows how the visual images slowly give way to literal representations, abbreviations, and finally, in the 17th century, to a more developed algebraic symbolism close to what we use in schools today [see: Note 1].
1. Mediaeval Algebra
The expansion of the Arab Empire into Asia Minor (Modern
Turkey) at the end of the 11th century led to a series of Crusades
to recapture the Holy Land. The major period of these military and
political disturbances lasted until the end of the 14th century. In
1340 the 'Black Death' spread into Western Europe killing some 40%
of the population by about 1370. In spite of these upheavals,
exchange of ideas and translations of Arab scholarship were brought
to Europe. After 1450 the printing press enabled many people to
read the Latin translations of Arab and Greek science.
Mediaeval Algebra in Western Europe was first learnt from the
works of al-Khowarizmi, Abu Kamil and Fibonacci. The algebra
consisted of simple linear and quadratic equations and a few cubic
equations, together with the methods for solving them; rules for
operating with positive and negative numbers, finding squares,
cubes and their roots; the rule of False Position (see
History of Algebra Part 1 ) and the Rule of Three (simple
proportion). These methods were applied to business and legal
problems. There was some justification of the solution using
diagrams, but mostly it was a matter of 'memorising the rules' and
applying them to standard problems.
Leonardo Fibonacci
(1170 - 1250)

Well known for his collection of mathematical techniques [see:
Note 2] and the promotion of the Hindu numeral system in the
Liber Abaci of 1202, he
also wrote Flos , a book
where he shows that the root of the cubic equation $10x + 2x^2 +
x^3 = 20$ can neither be a rational number, nor the square root of
a rational number [see: Note 3].
In his Book of Squares 1225 he turned much of Euclid's geometrical work into arithmetic, developing new ideas from Arab science, and other techniques used by the 'Abacus Masters' who taught commercial arithmetic [see: Note 4]. He organised the rules as a series of logical propositions and supported his arguments using proportional triangles, squares and rectangles, which as we have seen, are perfectly general.
Proposition
1 shows how the sum of the odd numbers always makes a
perfect square. In our notation, the substance of Leonardo's
argument is:$$(1+3+5+7)+9=(1+3+5+7+9)$$
Proposition 2
states "Any square number exceeds the square before it by the sum
of the roots." Leonardo's first example is simple:
$$5^2 - 4^2 = 25 - 16 \mbox{,
which is } 9 \mbox {, the sum of } 5 \mbox { and } 4\mbox {, which
are the roots of }25 \mbox{ and } 16.$$
Proposition 10
finds the sum of a sequence of square numbers: $$6(1^2 + 2^2 + 3^2
+.... + n^2) = n(n + 1)( 2n + 1)$$
Proposition 19
shows how to find numbers $A$, $B$, and $C$ such that: $$B^2 - B =
A^2 \mbox { and } B^2 + B = C^2$$
These and many other numerical relationships helped
mathematicians of the 15th and 16th centuries to develop techniques
for solving quadratic and cubic equations.
Jordanus de Nemore (1225 - 1260)
The mediaeval student's attitude towards solving equations was
quite different to ours. Today we arrange the algebra to isolate
the unknown and we make $x$ the 'subject' of the equation. In
Mediaeval times, the student worked with the known numbers in order
to find the 'root'. Jordanus' book, De Numeris Datis (Concerning given
numbers) was written about 1250 and is considered to be the first
advanced algebra written in Western Europe since Diophantos . It
offers a generalised treatment of quadratic, simultaneous and
proportional equations. For solving quadratics, the procedure
earlier described by Abu Kamil (c850 - c930) as 'completing the
square' was simplified, Part
1 (Section 7 Case 5) , and for a problem like 'A square and 10
of its roots equal 39' you make a square, and attach to two of its
sides rectangles whose length is half the number of roots, and
proceed to fill in the empty space with another square.
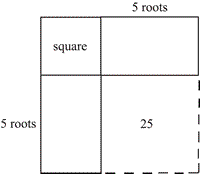
In the diagram, since the rectangles are $5$ roots long the dotted square must be $25$ roots. But the total of square and roots are given as $39$, so the side of the unknown square must be $3$, and the whole square $64$.
The 'Datis ' shows how, by analysis of
basic geometrical properties and using letters of the alphabet to
represent numerical relationships, it is possible to establish
generalised knowledge. Jordanus then illustrates each case with
numerical examples.
For example, in Book IV
Proposition 6, he shows that "If the ratio of two numbers
and the sum of their squares is known, then each of the numbers is
known." [see: Note 6].
In modern symbols, he proceeds like this:$$\mbox{Given, }x : y
= a \mbox { and } x^2 + y^2 = b$$
Let $d$ be the square of $x$, and $c$ the square of $y$,
and let $d + c$
be known , so we
have:
$$x : y = a, ~~~~~~~x^2 = d, ~~~~~~~y^2 = c, ~~\mbox {and so }
~~d + c = b $$
Now the ratio of $d$ to $c$ is the square of the ratio of $x$
to $y$, so $$\frac{d}{c}=\frac{x^2}{y^2}=a^2
~~~~~~~~\frac{d}{c}y^2=b-y^2 ~~~~~~~~
\left(\frac{d}{c}+1\right)y^2=b~~~~~~~~ \mbox {and so
}y=\sqrt{\frac{b}{\left(a^2+1\right)}}$$
$$ \text{For example, if
}\frac{x}{y}=2 \mbox { and } x^2+y^2=500 \mbox { then
}y=\sqrt{\frac{500}{\left(4+1\right)}} = 10\mbox {, and }x=20
~~~~~~~~~~~~~~~$$
The work of Jordanus was a significant change in the way
equations were tackled. Much more emphasis was given to the number
relationships that were based on proportional reasoning. It was the
understanding of these relationships that was so important to
Francois Viete later in the sixteenth century.
2. Early Renaissance Algebra
Nicolas Chuquet (1445 - 1488)
Nicolas Chuquet was described as an
'algoriste' and his manuscript on Le Triparty en la Science des Nombres
(1484) was known only to a few of his contemporaries. 'Triparty'
means three parts, and the first section was on Numbers and their
operations; the second on Surds $\left(3+\sqrt{5}\right)$ and Roots
of Surds $\sqrt{\left(3+\sqrt{5}\right)}$; and the third on
Algebra, where he invented special symbols for the unknown, squares
and cubes up to the fourth power, and a system of indices which
included $x^0 = 1$. He also used the first letters of operations
like p for plus and
m for minus. His algebra
was developed as a series of general methods and in this work
negative numbers appear as coefficients, exponents and solutions to
problems. His rules for solving arithmetic problems also used zero
and negative numbers. Unfortunately his work was little known, and
not published until 1880, but his ideas reappear in the early 17th
century.

Pacioli was a contemporary of Chuquet, and famous for the
Summa de Arithmetica, geometria,
proportioni et proportionibus (1494) and the Divina Proportione (1509) Pacioli's
works were important popular collections of current practical
mathematics and were more useful for passing on known techniques
and problems than for any original contributions. Pacioli is also
famous for publishing the first description of double entry
book-keeping where negative numbers had an obvious practical
significance as debts or losses, and numerous works on accounting
soon appeared in other languages, obviously copied from Pacioli
[see: Note 7].
3. Late Renaissance and Early Modern Algebra

Girolamo Cardano (1501
- 1576)
Cardano earned his living as a doctor and by casting
horoscopes; he wrote on probability and published other books but
his importance for us rests on his Artis Magnae sive de Regulis Algebraicis
Liber Unus (1545) "Of the Great Art, or the First Book on
the Rules of Algebra" the 'Ars Magna' as it is often called [see:
Note 8].
While the methods for solving quadratic problems were well
known as a collection of geometrically based proportional relations
and arithmetical algorithms, a unified and general approach was
still not commonly available.
The big unsolved problem of the time was finding solutions to
cubic equations. By this time mathematicians had identified about
13 different cases of cubic equations which included various
combinations of cubes, squares and numbers [see: Note 9]. The
Ars Magna contains the
proportional methods and rules that had been developed by
mathematicians before him, his own work was also a significant
contribution, and he acknowledged the discoveries of his
contemporaries.
Existing methods for solving cubic equations relied on finding
substitutions to reduce them to quadratics; many of these tricks
could only be applied to special cases. For example this is the
first problem in Chapter XXV:
When
the cube is equal to the first power and a constant, divide the
coefficient of x into two parts that the sum of each multiplied by
the square root of the other is half the constant of the equation.
The roots of these two parts added together make the value of
$x$.
Example: $x^3 = 10x + 24$
Solution: "Ten divides into two parts, $9$ and $1$, either of
which multiplied by the square root of the other makes $9$ and $3$,
the sum of which is $12$, one half of $24$. Therefore R $9$ plus R $1$ which are $3$ and $1$ added
together, produce $4$, the value of x."[see: Note 10]
Throughout the book, every
rule was written in Latin; the only notations used were
p
for plus and m for minus and an elaborate capital
R
for radix, to indicate square
roots.
 |
$~~~~~$ |  |
This symbol was invented by Regiomontanus (1436 - 1476) |
This symbol was not commonly used until about 1630 |
Discovering Imaginary Numbers
In Chapter XXXVII Cardano discusses the use of negative
numbers in calculations, and in Rule II appears his first use of negative square
roots.
The problem is to 'divide $10$ into two parts whose product is
$40$'
His method is exactly the same as the 'Babylonian Algorithm'
shown in
Part 1 (Teachers' notes 5) and if we think of the problem as: $
x(10 - x) = 40$, we have a quadratic equation $x^2 + 40 = 10x$
(squares and numbers equal roots) with $10$ as the coefficient of
$x$ which we divide in half, and
proceed with the algorithm .
Cardano gives two solutions
$5$p : R : m $15$ and $5$m : R : m $15~~$. [see: Note 11]
The product of these two results is, in fact $40$, and he
demonstrates how to solve four other problems that give negative
square roots. He was clearly mystified by these 'imaginary' square
roots of negative numbers, and this is still a problem for many who
meet them for the first time.
4. Introducing the 17th Century

Francois Viete (1540-1603)
In his two major works, In
Artem Analyticem Isagoge (Introduction to the Analytic Art,
1591) and De Potestatum
Resolutione (On the Numerical Resolution of Powers 1600)
Viete made probably the most important contributions to the
development of algebra at this time.
Viete used a consistent symbolic notation with vowels A, E, I,
O, U and Y for unknown quantities, and given terms by the letters
B, G, D and other consonants.
Addition and Subtraction used the symbols + and -. For Multiplication he used the word 'in' and for Division used the fraction bar. So $$\frac{\mbox {B in C}}{\mbox {AQ}} \mbox { meant } \frac{\mbox {BC}}{A^2}$$
Powers were N (for numerus - a pure number), Q
(quadratus - a square) C
(cubus - a cube) further
powers were expressed by combinations of these symbols, so QQ was a
fourth power, CQ, a fifth power and so on.
For Roots he used the symbol $L$ (for Latus - a side) and sometimes the
$R$ symbol . So $L9$ meant the square root
of $9$, and $LC 27$ meant the cube root of $27$.
All his equations were homogeneous - that means the dimensions
of all the terms in the equation had to be the same.
In the equation $~~~~AQ + AB = Z Q, ~~~~~AQ$ and $ZQ$
represent squares, and AB a rectangle.
Some of these notational ideas were already being used; for
example, Johannes Scheubel
(1494 - 1570) writing in 1551 used special combinations of symbols
for powers of the unknown:

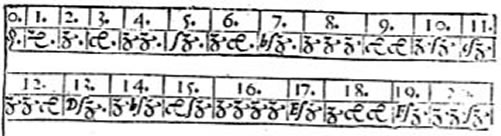
The English mathematician, Robert Recorde used the same notation
in his book [see: Note 12] on algebra in 1557 but describes the
powers of numbers in this way:
Using his literal notation, Viete exposed the
structural aspects of polynomial equations and gave solution
methods for whole classes of equations.
Viete's solution of quadratic equations used the three
proportional triangles in a semi-circle shown in Part
1 (Section 6. Greek Geometry)
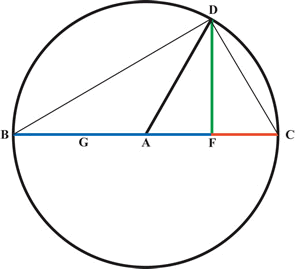
The equation: $ A$ quadratus $+ AB = Z $ quadratus or $ (A^2 + AB = Z^2) $, in
Viete's symbols is $AQ + AB = Z Q$, which can be written as
$A(A+B)=ZZ$ and rearranged as equal proportions becomes: $$
\frac{A}{Z}=\frac{Z}{(A+B)}$$
In the diagram there are three lines of increasing magnitude,
$FC, FD$ and $FB$.
$FC$ is $A$, $~~~~~FD$ is $Z~~$
and $FB$ is $A+B$
For three magnitudes in proportion, the well-known rule
is:
'the product of the extremes is
equal to the square of the mean'.
The lines $A$ and $(A+B)$ are the extremes and $Z$ is the mean .
For the equation $A^2 + 10A = 144, ~~~~~Z = 12 ~~~$ and $~~~A
: 12 = 12 : (A+10)$ so we have to find a number $A$, so that the
ratios are equal. The three numbers are $8, 12$ and $18$.
The Fundamental Theorem of Algebra

Thomas Harriot (c1560
- 1621) and Albert Girard
(1595-1632)
By this time, many mathematicians were working on similar
problems and developing their own notations. The most important of
these were Thomas Harriot, an English mathematician and explorer,
and Albert Girard, a Dutch Army Engineer. Harriot's work remains
mainly in manuscript form, even today. His Artis Analyticae Praxis (The Practice
of the Analytical Art) only appeared in 1661 well after his death,
but his papers show that he had developed a sophisticated notation,
almost like we use today, using $aa$ for $a^2, aaa$ for $a^3$ etc.
and through this realised that multiplying brackets like $(b - a)(c
- a)(d - a)$ led to a clear relationship between the roots and
coefficients of an equation.
The first explicit statement of the idea that every polynomial
equation of degree $n$ has $n$ roots appeared in 1629 in Girard's
L'Invention Nouvelle en
L'Algebre (A New Discovery in Algebra). Here, Girard states
his basic theorem,
"Every
algebraic equation .... admits of as many solutions as the
denomination of the highest quantity indicates ..."
Girard gave examples, but did not show how he derived his
theorem, and did not clearly account for 'imaginary' roots. The
search for a general proof occupied mathematicians for many years
to come.

Rene Descartes (1596 - 1650)
Even though many improvements in notation had begun to expose
the structure of algebraic equations, and begun to transform the
representation of the problems from geometric images to written
expressions, mathematicians still used geometry as a way of
demonstrating the 'truth' and generality of the algebra.
In 1637 he published his Discours de la Methode'... a work on
'how to undertake investigation to make ideas clear, and to seek
for truth in the sciences'. As an example of this method he
included La Geometrie
which states on the first page that,
"Any
problem in geometry can easily be reduced to such terms that a
knowledge of the length of certain straight lines is sufficient for
its construction."
Descartes demonstrates how this may be done:
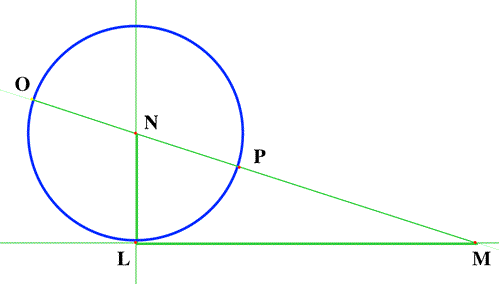
The equation is $z^2 \varpropto az-bb$. Construct $LM$ and
$LN$ so that $LM =b$ and $LN = \frac{a}{2}$
The unknown $z$, is $OM$. In triangle$NLM$, $$ NM^2
=\left(\frac{a}{2} \right)^2 + bb ~~\mbox { and }~~NM =
\sqrt{\left(\frac{a}{2} \right)^2 + bb}~~~ \mbox{. So }
z=\frac{a}{2}+\sqrt{\left(\frac{a}{2} \right)^2 + bb}.$$
However, Descartes still appealed to a theorem from Euclid
Book II Proposition 6 to justify his solution to the reader.
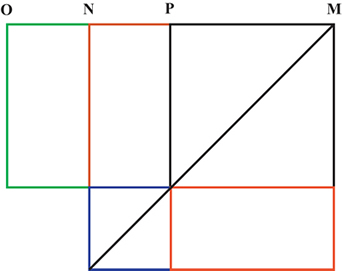
The rectangle contained by $OM$ and $PM$, plus the square on
$NP$, is equal in area to the square on $NM$. ($N$ bisects $OP$.)
The area of the green rectangle is the same as the areas of the red
rectangles.
$$ OM.PM + NP^2 = NM^2 $$
Here is Descartes' original description of the problem:

5. Notation and Representation [see: Note 13]
By the middle of the 17th Century the representation of
elementary algebraic problems and relations looked much as it is
today. The major factors influencing change were the printing press
that provided wider communication of ideas, and the slow
appreciation of the similarity in the structure of the algorithms
brought about by the changes in notation. Most of this happened in
the period from 1500 to 1650; by then the standard notation had
become generally accepted.
There were no clear stages in this process. Some historians
proposed a 'literal' stage where all the problems are written,
sometimes in very complicated language; a 'syncopated' stage with a
mixture of words and symbols; and a final 'symbolic' stage where
the mathematics consists only of symbols. But this is not the case,
even today when you look at a text, words are still there. Another
aspect was the technical
language . Translating from Greek and Arabic into Latin, and
then into the common language of a country, new words were invented
to describe new ideas, and were then taken over by others. For
example, the German for 'thing' or the unknown, was 'Die Coss', the
title of a book by Michael
Stifel (1487 - 1567). So, in England, algebra became known
as the Cossic Art .
Borrowing from the French, the pentagon was known as a cinqangle and so on. There are many
more examples among the writings of English mathematicians of the
16th and 17th centuries.
Representation of the objects, relationships, operations, and
the structure of processes together with the evolution of the
printing press, were the most important aspects which aided the
development of mathematics during this period.
The signs for Addition
and Subtraction first
appear in print in 1526, and the Equals sign appears in 1557. The cross
X for Multiplication is
later, about 1628; the Colon (: ) for Division in 1633 and the Obelus
($\div$) in 1659. The signs for inequality , > and < are first
used in 1631.
Square and other
roots start as the capital
R (as in the picture above)
in about 1465 and eventually our usual sign $\sqrt{}$ by 1630;
Powers were first expressed
by whole number indices in 1484 and had become widely accepted by
1637, and negative indices
also appear in 1484, but fractional indices not until
1676.
The symbols for the unknown and for constants are greatly varied. All kinds
of signs and combinations of signs were initially used. Jordanus
used letters to replace numbers as a sign of generality, Vieta was
the first to use vowels (A, E, I, O, U) for the unknown and
consonants (A, B, C, ...) for known quantities, and Descartes
introduced the convention of letters at the end of the alphabet (x,
y, z) for unknown and at the beginning (a, b, c) for known
quantities which is what we use today.
N.B.
Teachers' notes related to the history of algebra discussed
here can be found by clicking on the 'Notes' tab at the top of this
article .
Notes
- It is important to note that there were many people throughout this period from the 11th to the 17th century who made significant contributions to the story of the development of algebra, and have not been mentioned here. Further information can be found by consulting the references.
- We are very lucky that copies of Fibonacci's books have survived. The Liber Abaci (1202 ), Practica Geometriae (1220), Flos and the Book of Squares both produced in 1225 tell us a great deal about mathematics in the early Mediaeval period.
- Fibonnaci's approximate result is correct to nine decimal places. This equation was solved by Omar Khayyam (1048 - 1122) using the intersection of a circle with a hyperbola.
- The Abacus Schools were training courses for merchants in commercially useful arithmetic, but they also included 'puzzle problems'. Fibonacci has been mistakenly seen as the father of the Abacus Schools, but they existed well before his time.
- The Arithmetica of Diophantos (c200 - c284) had been translated and developed by the Arabs and was available in Latin at this time.
- I have taken this example from the translation by Barnabas Hughes, pages 167-168.
- It is interesting to contrast the social circumstances and the quality of the work of Chuquet and Pacioli. Chuquet had access to many mathematical works, and made the most of his opportunities in developing original ideas. However he was relatively isolated, hardly went outside his home city of Lyon, and his manuscript work was not printed at the time. Pacioli on the other hand was born into a commercial milleu in Italy, was known to two famous artists, Piero della Francesca and Leone Battista Alberti, was a tutor to the sons of powerful people in Venice and Rome, and had his books printed. This is not to denigrate Pacioli, but only to point out that different circumstances and the printing press played a large part in their fortunes.
- Most recent histories of mathematics give versions of the story of the solution of equations in 15th and 16th century Italy. Chapter 4 of John Derbyshire's Unknown Quantity gives a good account of the convolutions surrounding Cardan's work.
- We know that a cubic equation has three roots that are real or imaginary according to whether the graph cuts the x-axis in three places, touches the axis at a minimum, or cuts it only once. Clearly, these concepts were not available to Cardano.
- The substitution 'trick' comes from the works of Fibonacci and Jordanus: in our notation, if $x^3=ax+N$, let $a=f+g $ and let $ f \sqrt{g}+g\sqrt{f}=\frac{N}{2}$ then $x=\sqrt{f}+\sqrt{g}$
- $5+\sqrt{-15}$ and $5-\sqrt{-15}$
- Robert Recorde The Whetstone of Witte 1557. Another interesting aspect of the evolution of mathematical understanding is the development of a universal technical language. In England, many words were taken over from French (moitie meaning half) and German (zenzike meaning square). This is where the strange z symbol comes from.
- For websites with more detailed information on the development of notation see the list of References.
References
a) General sources covering the
mathematics of the Middle Ages and Renaissance:
Boyer, C. B. (1968) A
History of Mathematics . London. John Wiley. A popular book
with many reprints. Chapters XV and XVI cover the Middle Ages and
the Renaissance.
Cajori, F. A. (2007) A
History of Mathematical Notations 2 Vols. . This is the
principal source book for information in this area. Originally
published in 1928/9 by Open Court, there is a new paperback edition
available from Amazon at £ 17 for each volume. A bargain
for your college library.
Derbyshire, J. (2008) The
Unknown Quantity . London. Atlantic Books Now in paperback
at £9.99 this is a popular story of the problem of
finding the 'thing' of ancient algebra up to the 20th Century. The
Introduction and Part 1 up to page 94 1591cover the ideas in both
parts of this NRICH account. There are useful sections giving
reasonable straightforward explanations of the mathematics
involved.
Katz, Victor, J. (1999) (Second Edition, Corrected)
A History of Mathematics :
An Introduction Harlow,
England. Addison-Wesley The best and most comprehensive and
up-to-date general history of mathematics available. Chapter 9
'Algebra in the Renaissance' (pages 342 - 384) covers most of the
material in this article.
Kline, M. (1972) Mathematical Thought from Ancient to Modern
Times. Oxford. O.U.P. Before Katz, this was the best available and
has been reprinted a number of times. Chapters 11 to 13 on the
Renaissance and its mathematics are still very useful.
b) More specialised sources
available in translation:
Girolamo Cardano (1545) The
Great Art, or the Rules of Algebra. (Translated by R.
Witmer) 1968. M.I.T. Press.
Nicolas Chuquet, Renaissance
Mathematician (1985) Translated by Graham Flegg, Cynthia Hay
and Barbara Moss of Le Triparty
en la Science des Nombres . Lancaster Reidel Publishing
Company.
Rene Descartes (1637) La
Geometrie (Translated by D.E. Smith and Marcia Latham) 1954.
This Dover edition of the Geometry is still available. The English
translation is on one page, and a facsimile of the original French
on the facing page. The French is not too difficult, and the
notation for a quadratic equation virtually the same as
today.
Leonardo Fibonacci The Book
of Squares (Translated by L.E. Sigler ) 1987) London.
Academic Press.
Jordanus de Nemore De
Numeris Datis (Translated by Barnabas Hughes) 1981
University of California Press.
Recorde, Robert (1557) The
Whetstone of Witte From the original English Text.
Johannes Scheubel (1551) Algebrae Compendiosa From the Original
Latin Text Francois
Viete (1591) The Analytic
Art (Translated by R. Witmer) 1983 Kent State University
Press
Weblinks
The 'MACTUTOR ' is the
most comprehensive easily navigable website for the History of
Mathematics.
Here you can find the biographies of the mathematicians
mentioned in this article, including some detail of the relevant
mathematics involved.
The earliest use of various mathematical symbols can be found
at:
NRICH Links
Mathematical symbols:
Girard stated the Fundamental Theorem of Algebra, but the
proof for all kinds of polynomials was difficult to achieve.
Proof: A Brief Historical
Survey:
The search for general solutions to polynomial equations led
to the development of Galois Theory.
Introduction to Galois
Theory:
Here is an Algebra Problem from 1525.
Rudolff's Problem:
Diophantos' mathematics was translated by the Arabs in the
10th century. Many of his problems appeared in the work of
Fibonacci and Jordanus
Diophantine N-tuples:
The first diagram in this article represents some ideas that
are also found in Fibbonacci's Book of Squares
Picturing Pythagorean
Triples:
This is a modern treatment of the 'Imaginary' numbers
discovered by Cardano
What are Complex Numbers?