You may also like
A Problem of Time
Consider a watch face which has identical hands and identical marks for the hours. It is opposite to a mirror. When is the time as read direct and in the mirror exactly the same between 6 and 7?
Tricircle
The centre of the larger circle is at the midpoint of one side of an equilateral triangle and the circle touches the other two sides of the triangle. A smaller circle touches the larger circle and two sides of the triangle. If the small circle has radius 1 unit find the radius of the larger circle.
Attractive Tablecloths
Charlie likes tablecloths that use as many colours as possible, but insists that his tablecloths have some symmetry. Can you work out how many colours he needs for different tablecloth designs?
Age 14 to 16 Challenge Level:
This problem follows on from Translating Lines and Reflecting Lines.
I took the graph $y=4x+7$ and performed the four transformations shown on the cards below.
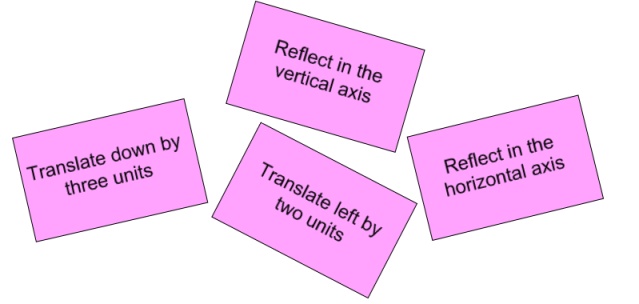
Unfortunately, I can't remember the order in which I carried out the four transformations, but I know that I ended up with the graph of $y=4x-2$.
Can you find an order in which I could have carried out the transformations?
There is more than one way of doing this - can you find them all?
Can you explain why different orders can lead to the same outcome?
What other lines could I have ended up with if I had performed the four transformations in a different order?
Copyright © 1997 - 2019.
University of Cambridge. All rights
reserved.
NRICH is part of the family of activities in the Millennium Mathematics Project.
NRICH is part of the family of activities in the Millennium Mathematics Project.