 Links to the NRICH website Home page
Links to the NRICH website Home page

30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
The Greedy Algorithm



- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
Why do this problem?
This problem follows on from Keep It Simple and Egyptian Fractions
These three problems together offer students an opportunity to engage with some mathematical ideas in depth and not just with the rather mechanical process of adding and subtracting fractions.
This problem in particular requires students to compare fractions and may deepen their understanding of their relative sizes.
Possible approach
Students should already have worked with fractions of the form $\frac{1}{n}$, $\frac{2}{n}$ and possibly $\frac{3}{n}$ and $\frac{4}{n}$ in Keep It Simple and Egyptian Fractions .
$\frac{4}{5} = \frac{1}{2} + \frac{1}{4} + \frac{1}{20}$ or
Key Questions
Is our fraction larger or smaller than $\frac{1}{2}$? How do we know?
....
Possible support
Students who need support in comparing the size of fractions might have to do some preliminary work on equivalent fractions.
Possible extension
Does the Greedy Algorithm always result in the sum with the fewest possible terms?
Can anyone find a counter example?
The Eye of Horus: often it was good enough to use only the fractions
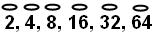
that represent $\frac{1}{2}$, $\frac{1}{4}$, $\frac{1}{8}$.... to get a fraction that is close enough to any specific fraction. Suggest that students pick some fractions and convert them to this form of Egyptian fraction.
How close does this method get to the target fraction?
Students might like to research how these particular fractions were written down in pictorial form.