Keep it simple
Can all unit fractions be written as the sum of two unit fractions?
Problem
Keep it Simple printable sheet
Unit fractions (fractions which have numerators of 1) can be written as the sum of two different unit fractions.
For example
$\frac{1}{2} = \frac{1}{3} + \frac{1}{6}$
Charlie thought he'd spotted a rule and made up some more examples.
$\frac{1}{2} = \frac{1}{10} + \frac{1}{20}$
$\frac{1}{3} = \frac{1}{4} + \frac{1}{12}$
$\frac{1}{3} = \frac{1}{7} + \frac{1}{21}$
$\frac{1}{4} = \frac{1}{5} + \frac{1}{20}$
Can you describe Charlie's rule?
The denominator of the last fraction is the product of the denominators of the first two fractions.
Are all his examples correct?
What do you notice about the sums that are correct?
Find some other correct examples.
How would you explain to Charlie how to generate lots of correct examples?
Alison started playing around with $\frac{1}{6}$ and was surprised to find that there wasn't just one way of doing this.
She found:
$\frac{1}{6} = \frac{1}{7} + \frac{1}{42}$
$\frac{1}{6} = \frac{1}{8} + \frac{1}{24}$
$\frac{1}{6} = \frac{1}{9} + \frac{1}{18}$
$\frac{1}{6} = \frac{1}{10} + \frac{1}{15}$
$\frac{1}{6} = \frac{1}{12} + \frac{1}{12}$ (BUT she realised this one didn't count because they were not different.)
Charlie tried to do the same with $\frac{1}{8}$. Can you finish Charlie's calculations to see which ones work?
$\frac{1}{8} = \frac{1}{9} + ?$
$\frac{1}{8} = \frac{1}{10} + ?$
$\frac{1}{8} = \frac{1}{11} + ?$
..........
Can all unit fractions be made in more than one way like this?
Choose different unit fractions of your own to test out your theories.
Getting Started
Try working systematically through all the possibilities.
$\frac{1}{8} = \frac{1}{9} + ?$
$\frac{1}{8} = \frac{1}{10} + ?$
$\frac{1}{8} = \frac{1}{11} + ?$
$\frac{1}{8} = \frac{1}{12} + ?$
$\frac{1}{8} = \frac{1}{13} + ?$
$\frac{1}{8} = \frac{1}{14} + ?$
$\frac{1}{8} = \frac{1}{15} + ?$
$\frac{1}{8} = \frac{1}{16} + ?$ (but this won't count)
Why is $\frac{1}{9}$ the first one you can use?
Why don't you need to go further than $\frac{1}{16}$?
Student Solutions
Well done to everybody who investigated this problem. Kizzy from Colyton Grammar School in England worked out in which circumstances Charlie's rule was true:
I figured out that as long as the first and second denominators are consecutive, then they can be times together to make the 3rd denominator. Therefore, the numerator is always 1 so this becomes super easy. Eg. $\frac{1}{3} = \frac{1}{4} + ?$ Because the 3 and 4 as denominators are consecutive they can times together to make 12. The answer would be $\frac{1}{12}$
Mohammad and Rayyan from Doha College in Qatar found a way of expressing this using algebra:
It appears that the first denominator of the first fraction in the sum is always one more than the denominator of the number we are adding to get, and the second denominator of the second fraction is always the product of the first fraction denominator and the sum denominator. This can be shown as a formula labelled "Charlie’s Law". Represented as $\frac{1}{n}=(\frac{1}{n+1})+\frac{1}{n(n+1)}$. Following this rule, we can generate new examples with absurdly large numbers, take for example $\frac{1}{678}$. We can figure out the sum using fractions by following the formula. First we generate a fraction of $\frac{1}{n+1}$ so we get $\frac{1}{679}$. Then we generate the second fraction $\frac{1}{n(n+1)}$ which is $\frac{1}{460362}$. In summary we get the sum, $\frac{1}{679}+\frac{1}{460362}$ which is equal to $\frac{1}{678}$. We can also verify this with a calculator. Overall, we can generate the sum of a unit fraction using more unit fractions by following this rule, of $\frac{1}{n}=(\frac{1}{n+1})+\frac{1}{n(n+1)}$.
I wonder why this rule works?
Hugh from Colyton Grammar School found a way to extend Charlie's rule to fractions where the denominators aren't consecutive:
The difference between the denominators is how much you divide by.
For example $\frac{1}{8}=\frac{1}{10}+\frac{1}{40}$
This is because you times 10 by 8 and divide by 2 because that is the difference of the 2 denominators, $\frac{1}{8}$ and $\frac{1}{10}$.
Jad from Kings' School Al Barsha in the UAE thought about representing this more general rule using algebra:
Multiply the denominators and divide the difference = $x$ times $y$ divided by $x-y$. For example $\frac{1}{12}=\frac{1}{13}+\frac{1}{156}$ because you multiple the denominators and divide it by the difference.
Is there a way we can prove that $\frac{1}{x}=\frac{1}{y}+\frac{1}{(xy/(x-y))}$?
Jenny from Tapton Secondary School in the UK began to think about which fractions can't be written as the sum of two different unit fractions in more than one way:
$\frac{1}{2}=\frac{1}{3}+\frac{1}{6}$
I really can't think of another way to do this
$\frac{1}{3}=\frac{1}{4}+\frac{1}{12}$
Again, I really can't think of another way. Let's say I'm right... There are a few number sequences with 2s and 3s (e.g. Fibonacci), but the one I think is most relevant is the prime numbers, as they have only 2 factors- thus, there should be fewer solutions (if they were the denominator). Let's test it out.
$\frac{1}{5}=\frac{1}{6}+\frac{1}{30}$
Well, the pattern is working (I think). Let's try a fraction with a composite (not prime) denominator.
$\frac{1}{12}=\frac{1}{13}+\frac{1}{156}$. Here's one. But I can think of more...
$\frac{1}{12}=\frac{1}{14}+\frac{1}{84}$
$\frac{1}{12}=\frac{1}{15}+\frac{1}{60}$
$\frac{1}{12}=\frac{1}{16}+\frac{1}{48}$
$\frac{1}{12}=\frac{1}{18}+\frac{1}{36}$
$\frac{1}{12}=\frac{1}{20}+\frac{1}{30}$
$\frac{1}{12}=\frac{1}{21}+\frac{1}{28}$
Here are some more that I think work, so there is more than one way of making all unit fractions with composite denominators (I think). I noticed something that further proves my statement - all of the fractions' denominators in each sum (except the 1st one) all have a factor in common with another fraction in the sum. Another interesting thing I found is that the last sum I wrote ($\frac{1}{12}=\frac{1}{21}+\frac{1}{28}$) doesn't have a common factor (above 1) between all three fractions, which is odd. Anyway, because all of the sums - excluding the one achieved with the formula - have common factors in between them, a sum with a prime denominator only has factors linking to the last fraction - there is no common factor (except 1) between the first two fractions (because a prime his only two factors~ 1 and itself).
No, not all unit fractions can be made in more than one way like this - unit fractions that have a prime denominator can only be made in one way (using the formula), while composite denominators can be made in several ways.
I think you're right, Jenny, but I don't think it's necessarily to do with all three denominators having a common factor - as you've spotted, this isn't always true.
Yawin from St Faith's School in Cambridge, UK agreed that fractions with prime denominators can't be written as the sum of different unit fractions in more than one way:
Not all unit fractions have this property. It doesn't work for prime denominators, like $\frac{1}{2}$, $\frac{1}{3}$, $\frac{1}{5}$, $\frac{1}{7}$, $\frac{1}{11}$, etc.
I started with $\frac{1}{2}$. The next fraction is $\frac{1}{3}$, so $\frac{1}{2}=\frac{1}{3}+\frac{1}{6}$.
Then I tried $\frac{1}{2}=\frac{1}{4}+\frac{1}{4}$ but the denominators were the same so it didn't count.
The reason why I stopped is that once I got to halfway, if I continue it will always be a greater fraction. For a fifth, for example, will use a non-unit fraction and for a sixth it will come up with a solution that we already have.
Take a look at Yawin's full solutions to see more of their ideas about this, including a table showing the different ways each fraction can be written as a sum of unit fractions.
Samuel from Renaissance College in Hong Kong showed why the $\frac{1}{n}=\frac{1}{n+1}+\frac{1}{n(n+1)}$ rule works, and began to think about extending this. The image below can be clicked on to enlarge it:

I wonder if we could generalise this method and end up at Jad's formula of $\frac{1}{x}=\frac{1}{y}+\frac{1}{(xy/(x-y))}$?
Ci Hui from Queensland Academies for Science Mathematics and Technology in Australia began to think about how to prove the more general rule with m and n:
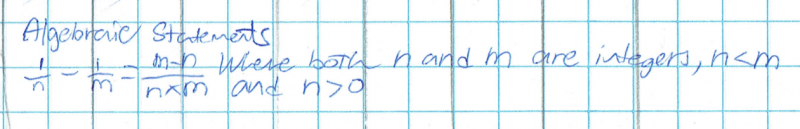
Can you see how this is equivalent to Jad's formula above?
Anirved, Aarya, Abheer, Ashaman, Dia, Mihika, Reyansh, Dhanwin, Darsh, Shiva, Siddhanth, Sunil, Nikhil, Karthik, Vishnuvardhan, Sehar, Dhruv, Aarya, Kanav, Atharvan, Keeya, Aaradhya, Rishaan, Tejas, Valerie, Varun, Kaumudi, Dhwani, Ira, Prathamesh, Adhrit, Delissaa and Riyansh from Ganit Kreeda, Vichar Vatika in India also had some similar ideas about this activity. They began by looking at a specific example, then worked to find a more general solution:
How to find all possible ways to write $\frac{1}{6}$ using equivalent fractions
They looked at different options for the denominator of the fraction after the equals sign:
$6+1$, $6+2$, $6+3$,…$6+6$. Or $6+m$ where $m$ can be anything from 1 to 6.
It will work only for those sums where the addend ($m$) is the factor of $(6+m)6 = 36 + 6m$.
We then generalised it for any unit fraction $\frac{1}{n}$.
According to above observation, it will work only for those sums, where $m$ (addend) is the factor of $(n+m)n$ or $m$ is a factor of $n^2 + nm$.
This is true only if $m$ divides $n^2$ (as $m$ divides $nm$).
Also we know that $m$ can take values from 1 to $n$. That means all factors of $n^2$ which are smaller than or equal to $n$, can be chosen as $m$.
This theory was tested for $\frac{1}{12}$.
First we anticipated all possibilities:
Now we have to find out $m$ such that $m$ divides $n(n+m)$ or $12(12+m)= 144 + 12m$…{as here $n=12$}
All factors of 144 smaller than or equal to 12 are 1,2,3,4,6,8,9,12.
So, there are 8 ways to write $\frac{1}{12}$. As we want distinct unit fractions, last one is not correct. So, there are 7 ways to write $\frac{1}{12}$ as sum of 2 distinct fractions.
Generalising this solution further, it looks like the number of ways of writing the fraction $\frac{1}{n}$ as a sum of two different unit fractions is the same as the number of factors of $n^2$ which are less than $n$. I wonder how this ties in with Jenny and Yawin's ideas about what happens when $n$ is prime?
If you'd like to see more of Ganit Kreeda's ideas about this problem, take a look at Ganit Kreeda's full solutions.
Thank you as well to the following students who sent in similar solutions to this problem: Luke from Renaissance College in Hong Kong; Dhruv from The Glasgow Academy in Scotland; Sophia from Guildford High School in England; Toby, Benedict, William, Frederick and William from Colyton Grammar School in the UK; Andres from Sequoyah School K-8 in Los Angeles, USA; Esa from Kings' School Al Barsha in the UAE; Yawin from St Faith's School in Cambridge, UK; Nina from CHPS in Australia; Hugh from Baldwin in the USA; Yannis, Esme and Ashleigh from ESF Renaissance College in Hong Kong; and Juan, Carlos, Adrian and Miriam from IES Maximo Laguna in Spain.
Teachers' Resources
Why do this problem?
This is the first problem in a set of three linked activities. Egyptian Fractions and The Greedy Algorithm follow on.
It's often difficult to find interesting contexts to consolidate addition and subtraction of fractions. This problem offers that, whilst also requiring students to develop and analyse different strategies and explain their findings.
Possible approach
Pose the initial part of the problem as it is set and ask the students to suggest what Charlie's rule might be. Allow some time for them to work out which sums are correct and ask them to modify Charlie's rule so that it always generates correct solutions. Working in pairs, invite students to generate some more examples that confirm their new rule. Collect some of these on the board for a general discusion. (With some classes this could lead to an algebraic explanation/proof.)
Alison's question offers an opportunity to involve the whole class in a collaborative activity. Talk through what Alison might have been thinking as she generated different pairs which worked. This might be an opportunity to talk to the class about the value of working systematically. How can Alison be sure that she has found all the possible pairs?
In pairs, ask students to choose their own unit fraction and find all the correct pairs.
Collect all results on the board and encourage students to share their strategies for finding all possible combinations.
Key questions
Can a unit fraction always be written as the sum of two different unit fractions?
Which unit fractions can only be written in one way?
What is the strategy for finding all the combinations of two unit fractions that add up to a third unit fraction?
Possible support
Some students may find it easier to contribute to the class discussion by working systematically to generate lots of unit sum calculations and highlighting any that result in a unit fraction as an answer.
For example
| $\frac{1}{6} + \frac{1}{7} = \frac{13}{42}$ | Image
|
| $\frac{1}{6} + \frac{1}{8} = \frac{7}{24}$ | Image
|
| ... | |
| $\frac{1}{6} + \frac{1}{12} = \frac{1}{4}$ | Image
|
Possible extension
Ask students to produce an algebraic or visual proof of Charlie's revised rule.
You may wish to move students on to Egyptian Fractions.
