Copyright © University of Cambridge. All rights reserved.
'Circles in Quadrilaterals' printed from https://nrich.maths.org/
Show menu
Circles in Quadrilaterals printable sheet
You may have come across the idea of a cyclic quadrilateral, where it is possible to draw a circle around the quadrilateral so that the circumference passes through all four vertices of the shape.
A tangential quadrilateral is one where it is possible to draw a circle inside it so that the circumference just touches all four sides of the shape.
Here are some examples of tangential quadrilaterals:
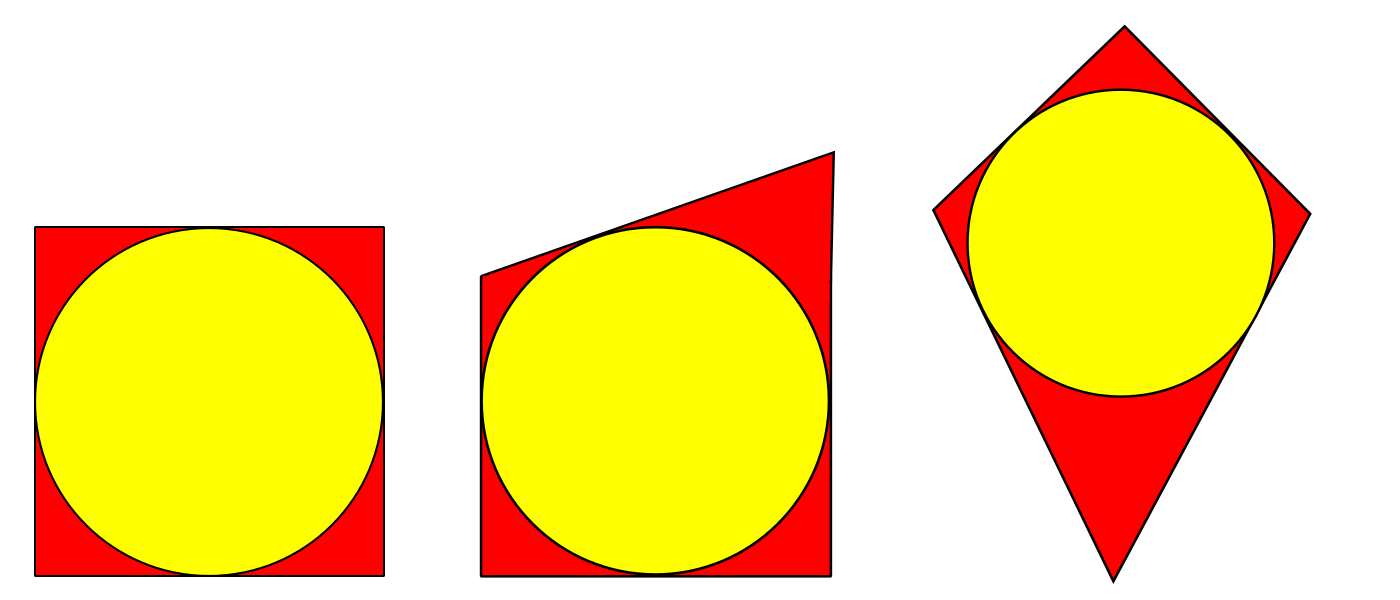
For each of the following types of quadrilaterals, decide whether it is always, sometimes or never possible to construct a circle inside which just touches all four sides:
- Square
- Rectangle
- Rhombus
- Parallelogram
- Kite
- Trapezium
If you decide always or never, you need to justify your decision with a convincing argument.
If you decide sometimes you need to be precise about when it is possible and when it is not possible, and why.