Pareq Exists
Problem
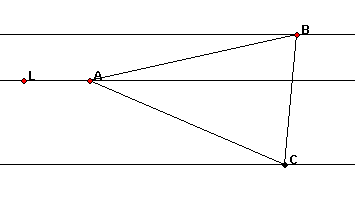
Prove that, given any three parallel lines, an equilateral triangle always exists with one vertex on each of the three lines. (In the problem 'Pareq Calc' the existence of the equilateral triangle was assumed.)
If you have Java enabled, it may help to use the dynamic diagram below which shows three parallel lines and the fixed point A on one of the lines. The points B and C are free to move along the other two parallel lines in such a way that the lengths AB and AC are always equal.
Click and drag the red points.
Getting Started

This is another tough nut mind bender, and we have to give a proof of existence. The conjecture is that, given any set of three parallel lines, there always exists an equilateral triangle with one of its vertices on each of the lines. The trouble with this sort of mathematics is that there are infinitely many possible cases. It means nothing that the conjecture holds true in every case we test because it might still break down in a case we have not tried. So what can be done? Playing with the dynamic diagram suggests that the length of BC changes - how does it change?
Student Solutions

We give two excellent and quite different methods of proof, one from Benjamin Girard, age 18, Lycee Pierre Bourdan, Gueret, France, and the other from Hyeyoun Chung, age 14, St Paul's Girls School, London.
BENJAMIN'S EXISTENCE PROOF
Benjamin gives a method for constructing the diagram using only a ruler and compasses (NB not a protractor).
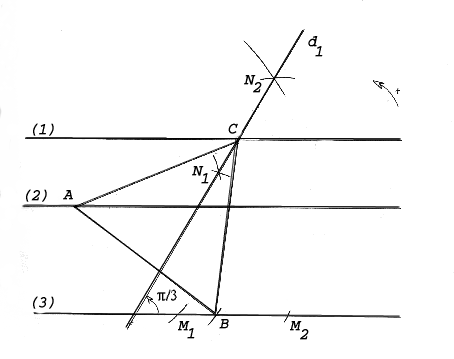
Let us call the three distinct parallels (1), (2) and (3) and choose a fixed point $A$ on the middle one. We shall construct the image $d_1$ of line (3) under the rotation $r$ by angle $\pi /3$ about the centre $A$.
To every point $M$ of (3) this rotation associates one point $N$ of $d_1$, such that
Line $d_1$ cuts (3) so it cuts (1). Let us call this intersection point $C$. So $C$ is on line (1), A is on line (2) and we know that a point $B$ on line (3), and only one, exists (because the rotation is bijective). So given any three parallel lines an equilateral triangle exists with one vertex on each of the three lines.
RULER AND COMPASS CONSTRUCTION
To construct the triangle by finding the positions of $B$ and $C$, first draw the line $d_1$. To do this, use compasses and, using any two radii, draw two arcs $s_1$ and $s_2$ with centre $A$ cutting line (3) at two points $M_1$ and $M_2$. Then with centre $M_1$ draw an arc of radius $AM_1$ to cut arc $s_1$ at $N_1$ and with centre $M_2$ draw an arc of radius $AM_2$ to cut arc $s_2$ at $N_2$. Draw the line $d_1$ through $N_1N_2$. Mark the point $C$ where the line $d_1$ cuts line (1). With centre $A$ draw an arc of radius $AC$ cutting line (3) at point $B$.
ANOTHER EXISTENCE PROOF
The dynamic geometry 'interactivity' suggested a proof based on a continuity argument.
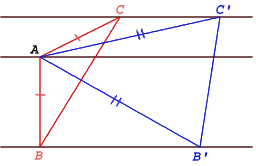
The point $A$ is fixed. As $B$ moves along line (3), point $C$ moves on line (1) such that $AB=AC$ making triangle $ABC$ isosceles. The shortest length for $AB$ occurs when $AB$ is perpendicular to the parallel lines and in this case $\angle BAC$ is obtuse. As $B$ moves the angle $BAC$ changes continuously getting smaller and there must be one position where $\angle BAC= {\pi \over 3}$ and triangle $ABC$ is equilateral.
Hyeyoun also uses a continuity argument, but quite a different one, rotating an equilateral triangle of a fixed size about one of its vertices so that three parallel lines through the vertices move continuously.
HYEYOUN'S PROOF
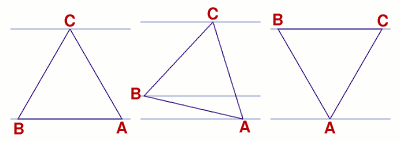
An equilateral triangle is positioned with its bottom edge along a horizontal line so that the vertices lie on three parallel lines, one through the uppermost vertex of the triangle, and the other two horizontal lines on top of each other and passing through the base of the equilateral triangle.
One vertex on the baseline is kept fixed and if the triangle is rotated about this point it can be imagined that the parallel lines through the other two vertices move with them, being translated upwards but remaining parallel.
If the triangle is rotated through an angle $\pi /3$ the middle of the three parallel lines leaves the bottom line and eventually merges with the top line. Therefore the ratio of the perpendicular distances between the parallel lines varies continuously from infinity to zero and so takes the required ratio $a:b$ at some point between. To achieve the actual distances $a$ and $b$ requires simply apply an enlargement.
Therefore it can be said that for every set of three parallel lines there is an equilateral triangle with a vertex on each line.
